このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
ガウス記号の利用
何をしているのかがさっぱりわからないです😭教えてください、、
どうしてガウス記号を使って求められるんですか??

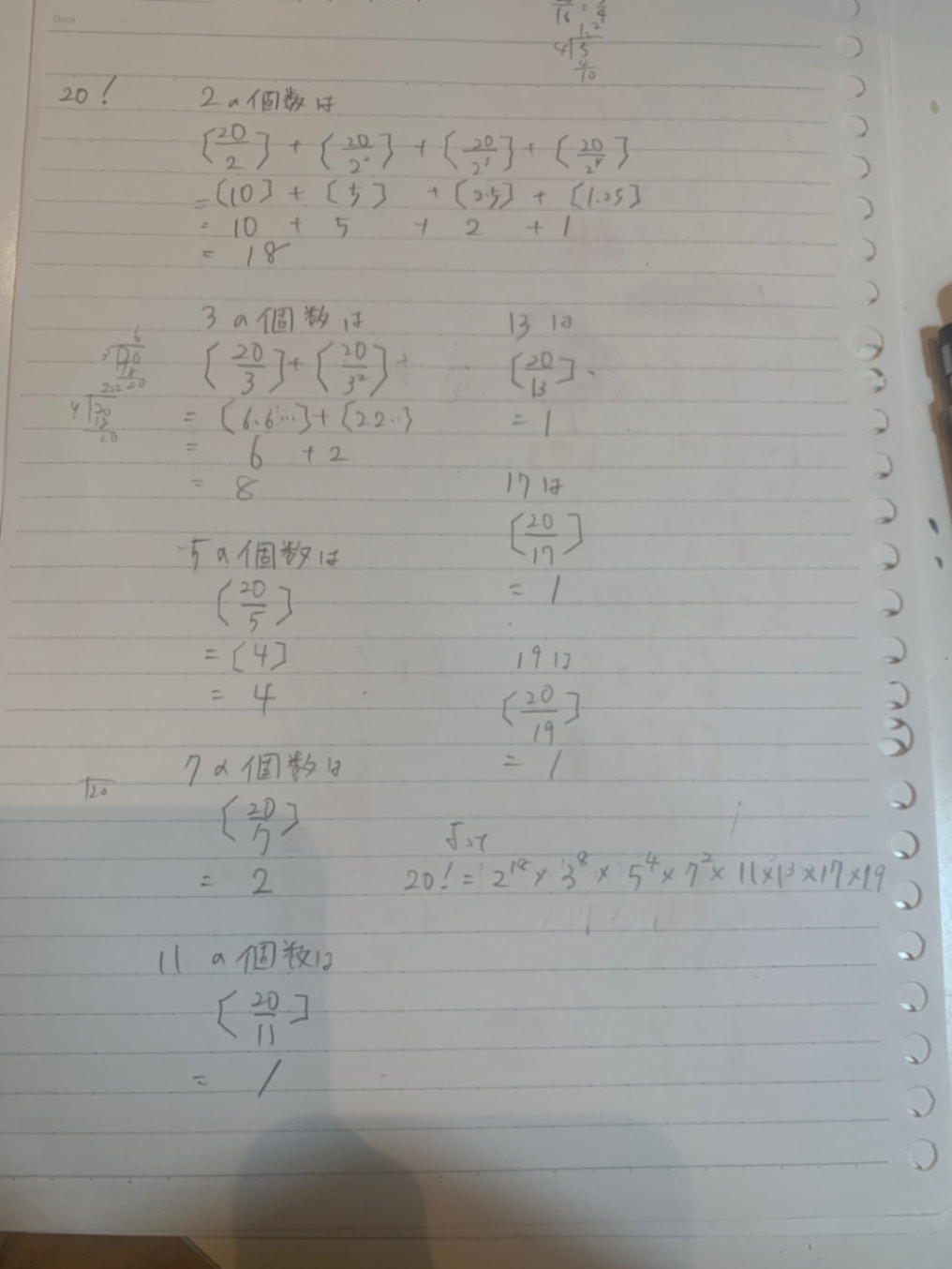
回答
百花さん、こんにちは。
1から1000までに7の倍数はいくつあるか?という問にはどう答えますか?
普通なら1000÷7=142余り6 という計算をして、商の142が7の倍数の個数ですよね。
これを小数で計算したら142.857…です。
ガウス記号というのは数の小数部分は捨てて整数部分だけをとる記号です。
(正式には「xを超えない最大の整数を[x]とあらわし、これをガウス記号という」です。意味は上に書いたことになります。)
[142.857…]=142 となり、割り算した時の商と同じです。
その解答ではカッコつけて、ガウス記号を持ち出していますが、そんな必要はありません。これも「やり方は1つじゃない!」です。
10までの素数は2,3,5,7しかないので、2の倍数の個数は10÷2=5で5個でいいし、4の倍数は10÷4=2余り2で2個、8の倍数は10÷8=1余り2で1個、3の倍数は10÷3=3余り1で3個、9の倍数は…5の倍数は…7の倍数は… とやっていけば算数で充分です。
Forcus のところに「素因数の個数→ガウス記号で表現せよ!」と書いてありますね。きれいな式で表現するのはたしかにガウス記号は便利です。でも具体的に数をもとめる時は、やることは算数の割り算です。なぜ算数の割り算が嫌われるかというと、数学では余りを扱うのはちょっと避けるのです。10÷3=3…1という式は数学的には等式ではありません。その=の記号は算数では使えますが、数学では左辺と右辺が等しいときでないと=は使わないからです。
結論:素因数の個数はガウス記号を使えば数学として式化できますが、算数で余りのある式を書いても解答としては問題ありません。
類題として(ちょっと大変ですが)20!とか30!を素因数分解せよっていうのをやってみます? 見ますよ。
これで大丈夫ですか?
あ、それとも2の倍数の個数に4の倍数の個数、8の倍数の個数を足しているところが疑問ですか?
なるほど!!!理解できました!!!ありがとうございます😭 20!やってみたので見てほしいです🙇
おめでとうございます!!完璧です💛
ありがとうございます😭