三角関数、図形

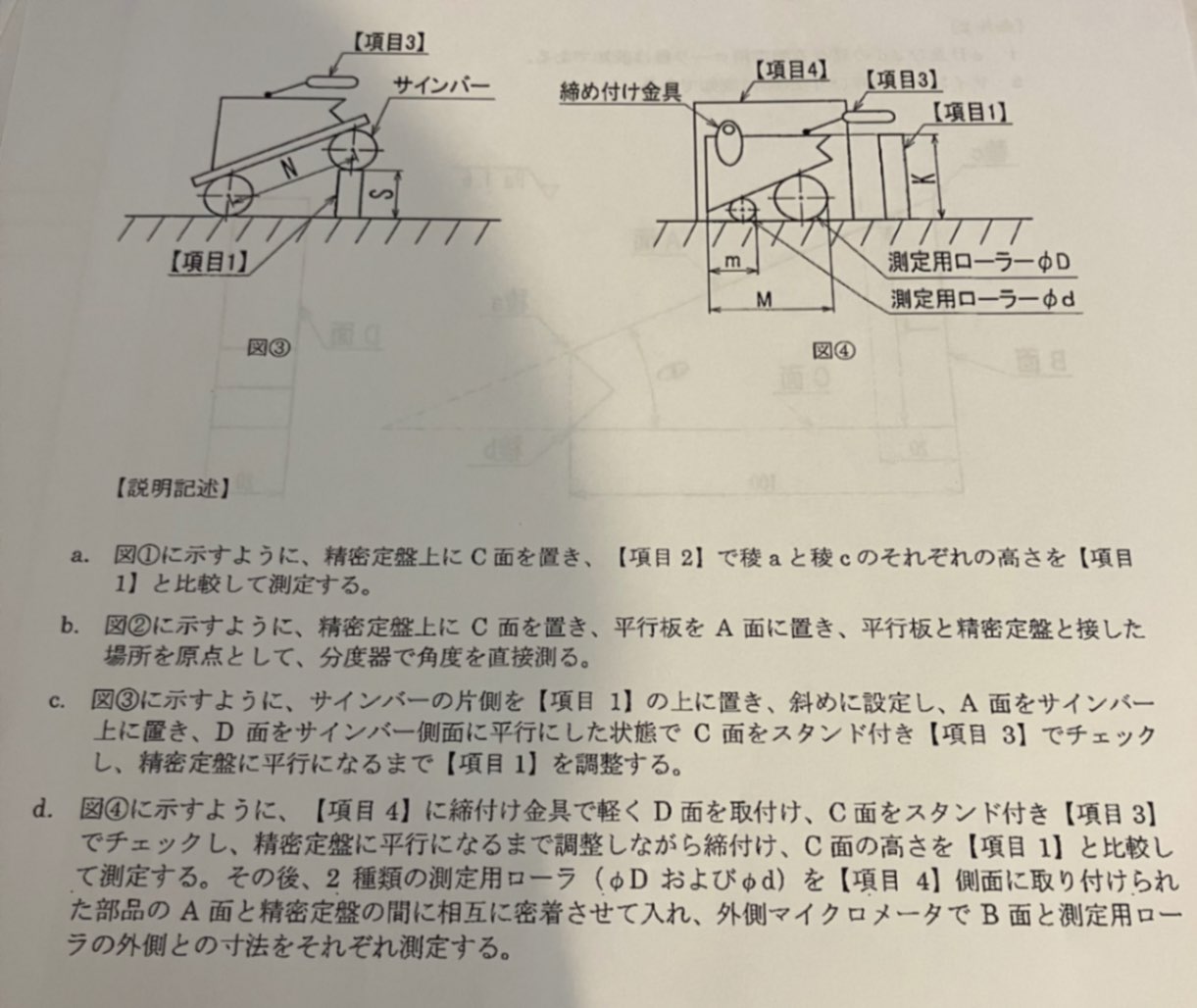
添付の問題について、Lの長さを求める時に設問4の答えがアなのですがどうしてそうなるのか理解できません。(図3.4を用いて) 図形で三角形書いて説明いただけると大変助かります。 宜しくお願いします。 因みにθの求める式はカ、キです。 ここはなんとなく理解できました。 (キはなぜtanに2が着くのかはわかりませんが)

【Lの長さについて】 図④において、Lは以下の式で求められる。 L=K-D/2-(ローラーφDの中心から垂直方向に面Aまでの長さ)+(底辺がM-D/2-20の直角三角形の高さ). ローラーφDの中心から垂直方向に面Aまでの長さは、この線分とローラーφDの中心から面Aに垂直に下した線分でできる直角三角形の斜辺である。 この直角三角形のローラーφDの中心にできる角はθだから、(ローラーφDの中心から垂直方向に面Aまでの長さ)=D/2 cosθ. (底辺がM-D/2-20の直角三角形の高さ)=(M-D/2-20) tanθ. ∴L=K-D/2-D/2 cosθ+(M-D/2-20) tanθ. 【キのtan^(-1)に2がつく理由】 ローラーφDの中心とローラーφdの中心を結ぶ線分が斜辺となる直角三角形を考えると、キの式が求められる。 このとき、この直角三角形の底辺と斜辺がなす角は、θ/2.　※斜辺が角の二等分線になっていることに注意。 tan^(-1)[(d/2-D/2)/{m-M-(d/2-D/2)}]=θ/2. ∴θ=2tan^(-1)[(d/2-D/2)/{m-M-(d/2-D/2)}].