このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
不等式の証明
⑴この後どのように変形したら解答のようになるのか分かりません、、
⑵どうして赤線の不等式が成り立つんですか??
宜しくお願いいたします🙇

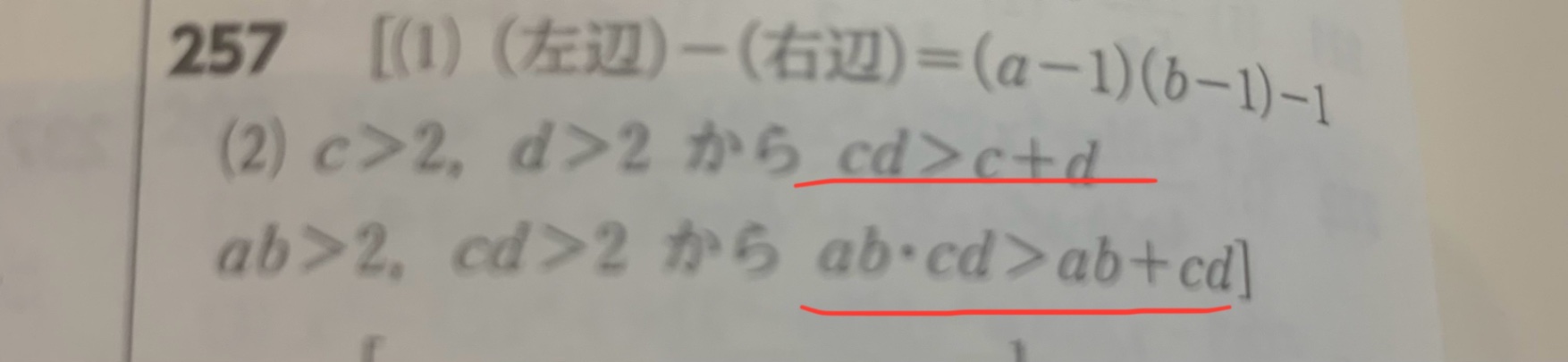


回答
百花さん、こんばんは。
(1)がいやなやつで、(2)は(1)を使うだけなんです。
(1)の変形はちょっと無理やりなので難しいです。
$ab-a-b+1$ の因数分解は大丈夫ですか?
$=a(b-1)-(b-1)=(b-1)(a-1)$ となります。
これに見覚えがあれば
$ab-a-b=ab-a-b+1-1=(a-1)(b-1)-1$ とやれますが、見覚えがないとなかなかできるものではありません。
このあと、$a-1>1,b-1>1$ だから $(a-1)(b-1)>1$ よって $(a-1)(b-1)-1>0$ として、与不等式が証明できます。
でも、ちょっと手間はかかりますが、別な自然な方法もありますよ。
a、bは2より大きいので、 $a=2+p,b=2+q (p,q>0)$ と置くことができますので、
左辺ー右辺=$ab-a-b$ にこれを代入して計算すれば自然に>0が示せます。やってみてください。
このほうが自然ですので納得しやすいと思います。やり方はいろいろあるのです。
(2)は(1)に当てはめただけなんです。
(1)は2より大きい2つの数について成り立つことを証明したのですから、2より大きいcとdでも成り立ちます。上の赤線部です。
$ab>a+b>4>2$ だから当然 $ab>2$ で、同様に $cd>2$ ですから、(1)のa、bにabとcdを当てはめることができます。下の赤線のところがそれですね。
これで大丈夫ですか?
ありがとうございます!よくわかりました!!!!もう一つの方もやってみたので見てほしいです🙇宜しくお願いします🥺
OKです!!それで大丈夫です。
ありがとうございます❣️