三角比の問題

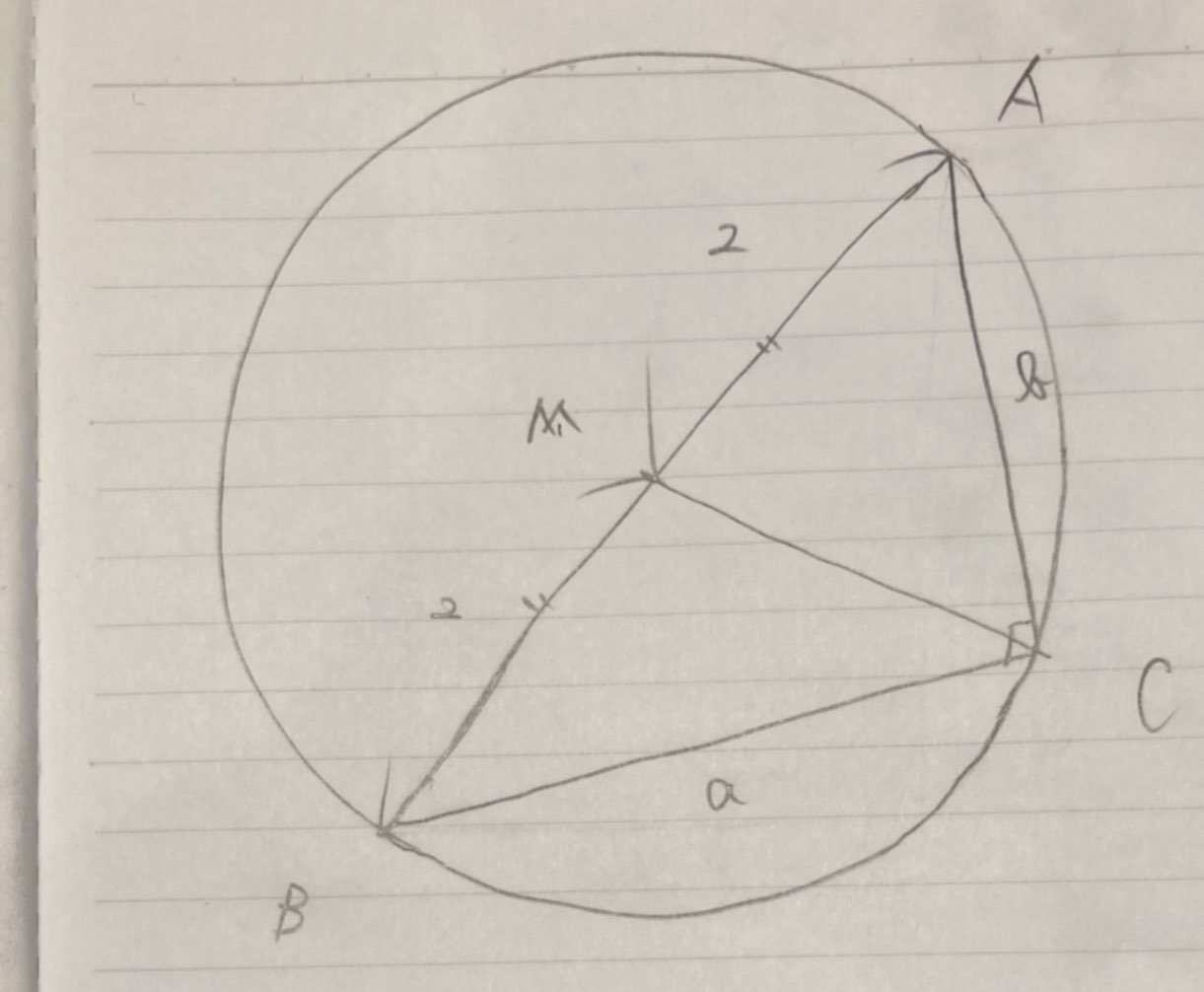
△ABCにおいて、角C=90°、辺ABの中点をM、辺BCの長さをa、辺ACの長さをbとする。△ABCが半径2の円に内接し 等式「a sinA = 2b sinB」が成り立っているとき、aの値は( 1 )であり cosBMCの値は( 2 )である。 分かる方いらっしゃいましたら教えていただけますと幸いです。

田中 洋介 さん、こんにちは。初めての方ですね。よろしく。 ここは質問箱なので…丸投げは…ちょっと…なんです。 質問の時は、自分はここまでやったのだけれど、この先が分からないのでヒントをくれとか、なるべく具体的に聞いてください。あなたがすでに分かっていることまで書くのはこちらも疲れが増しますので（笑）。一番いいのはあなたのノートを写真でアップしてくれることです。そうすれば的確なアドバイスができます。次回からはそうしてくださいね。 ここでは会話型を目指しています。あなたのような質問の時は、まずヒントというか方針を書きますので、その方針で自分でやってみてください。 まず、∠Cが直角であることからABは直径でMは円の中心であることが分かります（大丈夫ですか？）。 AB=4ですから、まずは三平方の定理を当てはめます。この辺りまではやってみたのかな？（ノートが見たい！） このままではa,bの式になっただけなので、もう一つ式が必要です。それが与式！ さて、これをどうにかするところまではいったのかな？（ノートが見たい！） サインが入った関係式なので、使うのは正弦定理じゃないかと想像して使ってみてください。sinAやsinBの代わりにa/4やb/4を使うのは分かりますか？これでa,bの式になります。この2つの式があれば、a,bの値は求まりますね。やってみてください。 次、∠BMCのコサインです。コサインと来れば余弦定理！三角形BMCで∠BMCに関する余弦定理を当てはめればコサインの値は求まります。じゃ、これも計算してみてください。 正解はお持ちですか？出た答と合わないようなときには見ますので、写真をアップしてくださいね。 これでやってみてください。これを読んだら、わかったとか、できたとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。返事がないと、せっかく書いたものを読んでくれたのかどうか、書いたものが役に立ったのかどうか、こちらではわからないのです。コメントよろしく。