このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
高校数学 三角関数 色々な公式の単元の問題がわかりません。
写真一枚目の(2)がわかりません。
三角関数の合成でasinθ+bcosθ=√a^2+b^2 (θ+α) となるのは理解しているのですが、解答の2行目から3行目に移るところでなぜsinθcos(-π/4)……となるのかがわかりません。
わかりやすく教えていただきたいです。お願い致します🙇🙇

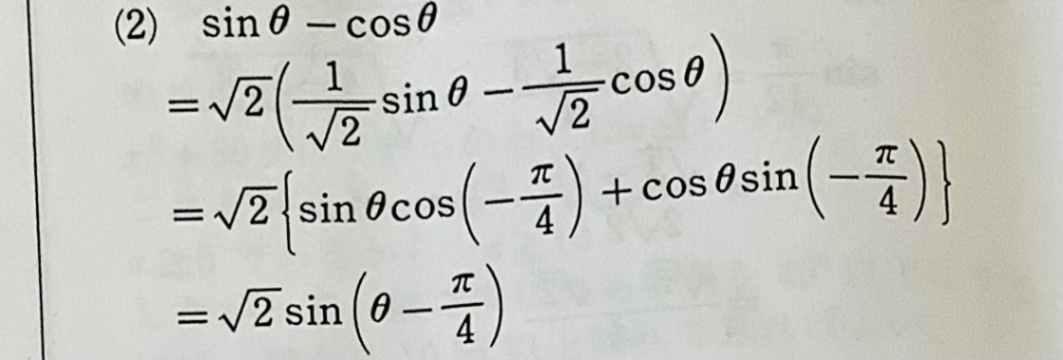
回答
Kano Momoka さん、こんにちは。初めての方ですね。よろしく。
三角関数のところは公式みたいなのがたくさん出てくるので大変ですね。
三角関数の合成で使うおおもとの公式は
$\sin (\theta +\alpha)=\sin \theta \cos \alpha +\cos \theta \sin \alpha$
です。これを左右逆にした
$\sin \theta \cos \alpha +\cos \theta \sin \alpha=\sin (\theta +\alpha)$
の左辺に合うように式を変形していくのです。
$a\sin \theta+b\cos\theta$ を $\sin \theta\cdot a+\cos\theta\cdot b$ …①
と見て、a,bの部分がある角のコサイン、サインになるように変形していきます。$a^2+b^2$ は1ではないので、a,bを $\sqrt{a^2+b^2}$ で割ったものなら、$\left(\dfrac{a}{\sqrt{a^2+b^2}}\right)^2+\left(\dfrac{b}{\sqrt{a^2+b^2}}\right)^2=1$ になるので、それを利用します。
そのために、 $\sqrt{a^2+b^2}$ を前に出して
$a\sin \theta+b\cos\theta=①=\sqrt{a^2+b^2}\left(\sin \theta \dfrac{a}{\sqrt{a^2+b^2}}+\cos \theta \dfrac{b}{\sqrt{a^2+b^2}}\right)$
この式の $\dfrac{a}{\sqrt{a^2+b^2}}$ が $ \cos\alpha$ で、$ \dfrac{b}{\sqrt{a^2+b^2}}$が $ \sin\alpha$ であるような角αを見つけます。
あなたの質問の問題では、
$1\cdot \sin \theta+(-1)\cos \theta=\sin \theta \cdot 1+\cos \theta \cdot (-1)$ となりますから、a=1、b=-1です。
これで合成の公式に入れれば
$=\sqrt{2}\left( \sin \theta \dfrac{1}{\sqrt{2}}+\cos \theta (-\dfrac{1}{\sqrt{2}}\right)$ …①
となるので、$\cos \alpha=\dfrac{1}{\sqrt{2}}, \sin\alpha=-\dfrac{1}{\sqrt{2}}$ となるようなαを求めます。
それは $\alpha=-\dfrac{\pi}{4}$ となります!
よって
$=\sqrt{2}\left( \sin \theta \cos (-\dfrac{\pi}{4})+\cos \theta \sin (-\dfrac{\pi}{4})\right)$
$=\sqrt{2}\sin\left(\theta+(-\dfrac{\pi}{4})\right)$
$=\sqrt{2}\sin\left(\theta-\dfrac{\pi}{4}\right)$
となるのです。
いまここでは、超ていねいな式変形を書きましたので、面倒くさいと感じるかもしれませんが、慣れてくればこんなに考えなくてもいけるようになりますよ!
別解としては、初めの問題がサインひくコサインなので、加法定理の
$\sin(\theta-\alpha)=\sin\theta\cos\alpha-\cos\theta\sin\alpha$
を使う手もあります。
これで大丈夫ですか?ここでは会話型を目指しています。これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。返事がないと、せっかく書いたものを読んでくれたのかどうか、書いたものが役に立ったのかどうか、こちらではわからないのです。コメントよろしく。