対数関数グラフ

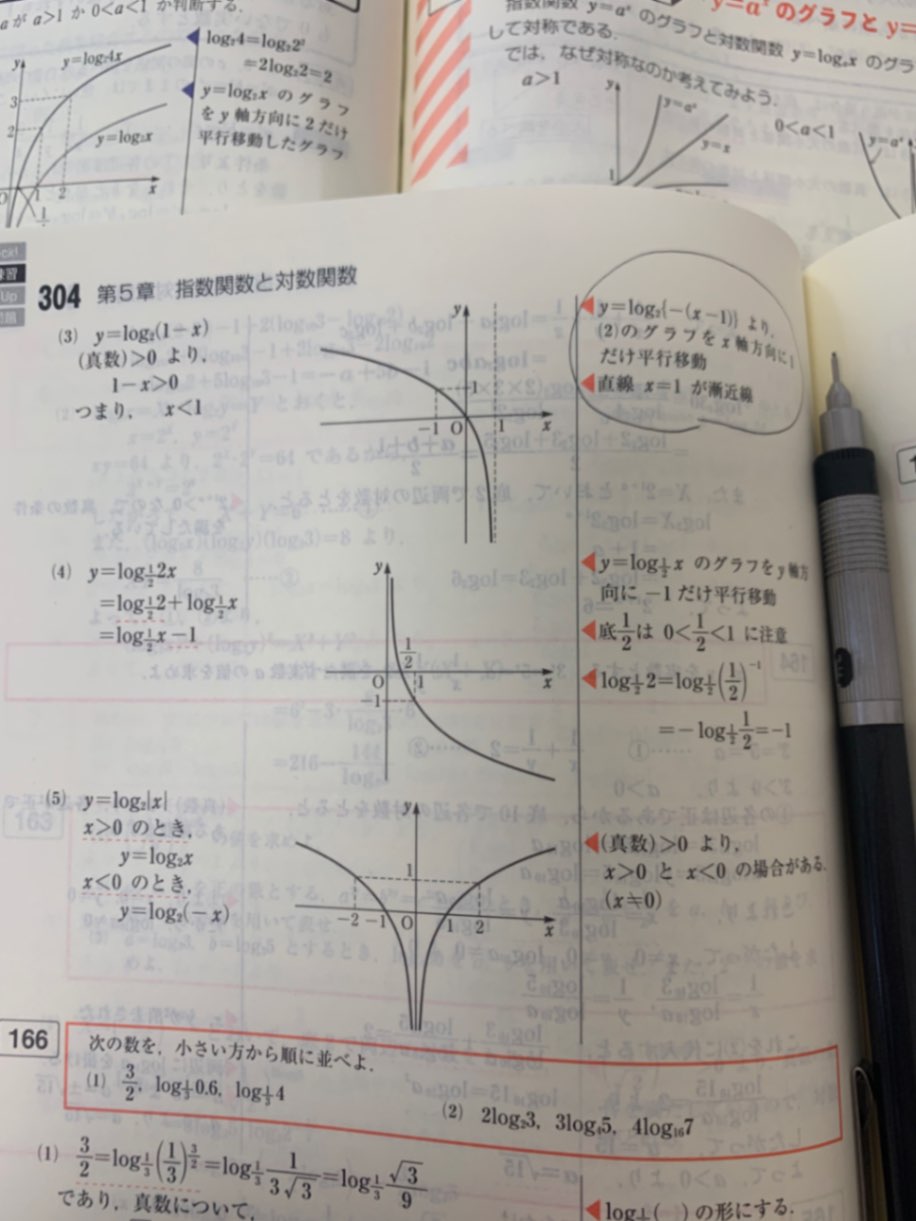
4がわかりません。自分でもやってみたのですがグラフにできませんでした。お願いします🙇 またいくつか質問を書き込んだのでそこも教えてほしいです。

百花さん、こんばんは。指数・対数で苦労しているみたいですね。対数は多くの人が悩むところです。なんとか慣れるまで頑張ってください。 まず（４）ですが、私の考えでは模範解答よりもあなたのやり方の方を教えてきました。底が１より小さいときは考えにくいので、梯の変換で１より大きくしてから考えた方が楽です。あなたが底を２にしたのは大正解です。 $y=-\log_2 2x$ はもう少し簡単にできます。 $y=-\log_2 2x=-(\log_2 2+\log_2 x)=-\log_2 x-1$ この式から、このグラフは $y=\log_2 x$ のグラフをｘ軸に関して対称に移動してから、ｙ軸方向にー１だけ平行移動したものだ！というふうにつかんだ方がグラフは描きやすいです。 「ｘ軸に関して対称に移動してから、ｙ軸方向にー１だけ平行移動したもの」になるのはわかりますか？ グラフの移動に関して一般的な公式（？）をまとめます。 ①$y=f(x-a)$ のグラフは$y=f(x)$ のグラフをⅹ軸方向にaだけ平行移動したもの ②$y=f(x)+b$ のグラフは$y=f(x)$ のグラフをy軸方向にbだけ平行移動したもの まとめると $y=f(x-a)+b$ のグラフは$y=f(x)$ のグラフをⅹ軸方向にa、y軸方向にbだけ平行移動したものになります。 ③$y=-f(x)$ のグラフは$y=f(x)$ のグラフをⅹ軸に関して線対称移動したもの、つまりⅹ軸を軸にして上下を逆にしたものになる ④$y=f(-x)$ のグラフは$y=f(x)$ のグラフをy軸に関して線対称移動したもの、つまりy軸を軸にして左右を逆にしたものになる ⑤$y=-f(-x)$ のグラフは$y=f(x)$ のグラフをⅹ軸、y軸に関して線対称移動したもの、つまり原点に関して点対称移動したものになる このへんのことはもう習いましたよね。数Ⅰの2次関数あたりでやったのかなぁ。でもなかなか難しい個所です。 これがわかっていたら、いくつかの質問に答えられますね。 （４）は $y=f(x)$ のグラフを$y=-f(x)$ のグラフにして（③ⅹ軸対称移動）、次に②の考えでｂがー１になった場合だからｙ軸方向にー１だけ下げればいいのです。 次。$y=\log_a x$ は、0<a<1のときは減少関数、a＞１の時は増加関数であることは大丈夫ですか？…（A) 質問の関数は底は１より大きいけれど$y=\log_a x$ ではないです。マイナスが付いています。だから（A)は使えません。上の③を使って $y=\log_2 x$ のグラフをⅹ軸に関して上下反転してみれば、減少関数のグラフになってるでしょ？ 最後のは $y=\log_2 (-x)$ だから上の ④の形で、$y=\log_2 x$ 　のグラフをｙ軸に関して左右逆にしたものだから、やっぱり減少関数。 真ん中のは $y=\log_2 -(x-1)$ だから最後のやつのｘのところがｘ－１になっているので、上の①より最後のやつのグラフをⅹ軸方向に１だけ右に平行移動したものだから、やはり減少関数ですね。 ぱっと見で分かりにくいものはこうして順に考えていきますよ。 これで大丈夫ですか？グラフの平行移動や線対称移動、点対称移動はけっこう大事なのでよく考えてください。分かりにくいときは、できればこの問題ではなく単にグラフの移動に関してだけを先生に直接質問して、じっくり対面で説明してもらうのが最良なんですが…。 これで大丈夫ですか？