連分数

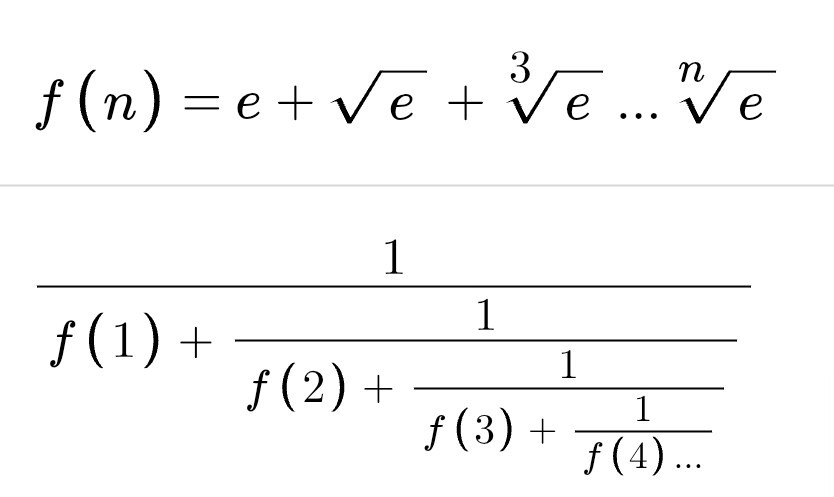
問題解決のためのヒントがほしいです。 I2(2)/ I1(2)　※Iα(x)はベッセル関数 のような答えになりそうですが… どんな学習(あるいは分野)の問題ですか？

コメントありがとうございます。この問題の分野ということですが、もともとは、友人が出してきた問題でして…一応友人は工学系なのですが、彼はいろいろな分野の数学の問題に進んで取り組んだりしているので、直接本人に聞かないとわから　ないかもしれません。 この問題自体は他人からのものにすぎないかもしれませんが、どうにも自分の知識から答えを導こうとしたあまりにです。しかし、問題を出すのであればそれがどの分野のものかを把握しておくべきだったと思います…盲点でした。 ヒントとなるものは、おそらく、現状わかっているものでlim(n→∞)f(n)=∞となることくらいでしょうか？こんなものは簡単にわかるようなことですが… 正直、自分はこの問題をさぞ甘く見ていたと思います。最初のコメントが来る頃には、議論が可能なほどにこの問題について深めようと考えていましたが、いつも向き合う未知の問題以上にあまりにも未知の問題すぎるがために、今でもまだ迷っています。 それにしても、ベッセル関数とはどういった関数なのでしょうか？過去に何度か聞いたことがある気がします…

こちらこそコメントありがとうございます。 面白い問題に挑戦できて楽しいです。 さて、ベッセル関数は、ウィキペディアでも調べることができる関数なので調べてもらえればよいのですが、 今回興味深いのは、ベッセル関数を使って、ある連分数を表すことができるという事実です。 【事実】連分数[2,3,4,5,…]=I1(2)/ I2(2).　※Iα(x)はベッセル関数 以下、あなたの問題の連分数について考察したことになります。 ①問題の連分数は収束すると思われる。 (理由)問題の連分数をf(N)まで考えたものを、aNとする。簡単な計算から、a2<a4<a5<a3<a1. 帰納法を使えば、a2<a4<…<a(2m)<…<a(2m-1)<…<a5<a3<a1. {a(2m)}は上に有界かつ単調増加だから、収束値αをもつ。 {a(2m-1)}は下に有界かつ単調減少だから、収束値βをもつ。 α=βかどうかはどうしましょうか… ②仮に求める連分数が収束値αをもつとし、このαを、分母の数が整数の正則連分数で表すことを考える。 α≒[0,2,4,5,6,8,…]≒1/(I1(2)/ I2(2))=I2(2)/ I1(2).　※近似値ですが…

間違っているかもしれませんが、一応求まりました。答えは、(-e^2+e√e^2+4/e)/2ではないでしょうか。解法はとりあえず画像かなにかで送信します。

失礼。答えをミスりました。(1+e+√(1+e)^2+4e)/2eでした。