このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
グラフ 微分



回答
なるほど!ありがとうございます!
ちなみになのですが、斜めに原点に突っ込むこともありますか?
一つ上の問題のなのですが、これもx=0のとき、y’=0だからx=0のところで平らになってますか?
①どこであろうとy’の値が0になるところではグラフは一瞬ですが水平になります。y’≠0のところではグラフは斜めになっていますよ。x=0でy’≠0なら原点に斜めに突っ込みます(笑)。 ②どの問題?2枚目の写真の(1)も3枚目の(1)も、x=0でy’=0ですから一瞬平らというか水平になりますよ。x=0を境にy’の符号が変わ絵うようなら、そこで極値をとります。グラフは山の頂上または谷の底になっていますね。y’の符号が変わらないときは、最初の質問のグラフのようになるのです。y’=0でも極値をとりません。 これで大丈夫ですか?
ポイントはy’の符号が変わる時に極値を取るということですね! また、y’=0ときとは接線の傾きが0の時だからどこであろうと、一瞬グラフが水平になるということですね!
そうです!そうです!!
すみませんもう一個いいですか?
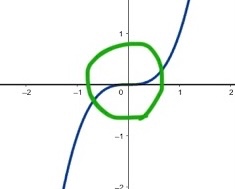
y’=0ときとは接線の傾きが0の時だからどこであろうと、一瞬グラフが水平になるということですね! →のはずなのに、写真の青丸のところは水平になっているように見えないのですが、、、
この時もy’=0なのだから水平になるんじゃないんですか、、😭
あ、なってますよ!谷底では接線は水平で、グラフは一瞬だけですが水平なのです。実際には曲線ですから「水平な直線部分」はないですよ。これで大丈夫ですか?
減少から増加にかわる瞬間は接線は水平。増加から減少になるときも接線は水平。グラフは一瞬ですが水平。ただし一瞬なので、絵では見えません。放物線の頂点のところと同じです。
ありがとうございます! グラフは水平になってはいるけれど、一瞬だから放物線の頂点と同じってことであってますか? グラフが明らかに水平になるのはy’=0の前後でy’の符号が変わらないときっていう考えでいいですか?
あれ?ちょっと違います。「グラフが水平になる」という言い方は本来おかしいのですが、y=x³のグラフはもう習って書いたと思いますが、あのグラフの減点の付近とy=x²のグラフの減点付近はどちらのグラフも一瞬水平になっていますよ。「左のほう」から見ていくと、3乗の方は増加しながら原点を通過し、その瞬間だけ水平です。見えませんが。その後も増加が再開しています。y’の符号は0の前後で正です。2乗の方は減少しながら原点を通過し、その瞬間だけ水平です。見えませんが。その後は増加に転じて極小値を作ります。 なかなかことばでの説明は難しいなぁ。わかるかなぁ?
あーなるほど!!!ちょっとわかった気がします!!!!! わたしは今までグラフについて誤ったイメージをもっていたようです、、、 引きで見るとよくわからないけれど拡大してみると、y=x²もy=x³も原点付近で一瞬水平になっているんですね! 追加させていただいた写真のかんじですね!
そうです、そうです!!それで大丈夫です。分かったようですね!
最後まで丁寧に教えてくださり本当にありがとうございました😍
どういたしまして。楽しいです。