このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
理数グランプリーわからない問題
いつもお世話になっております。打方佑弥です。
この度、福井理数グランプリ中学部門(数学)に出場させていただくことになりました。
そこで過去問を解いていたところ、解説を読んでもわからない問題に遭遇してしまいました…
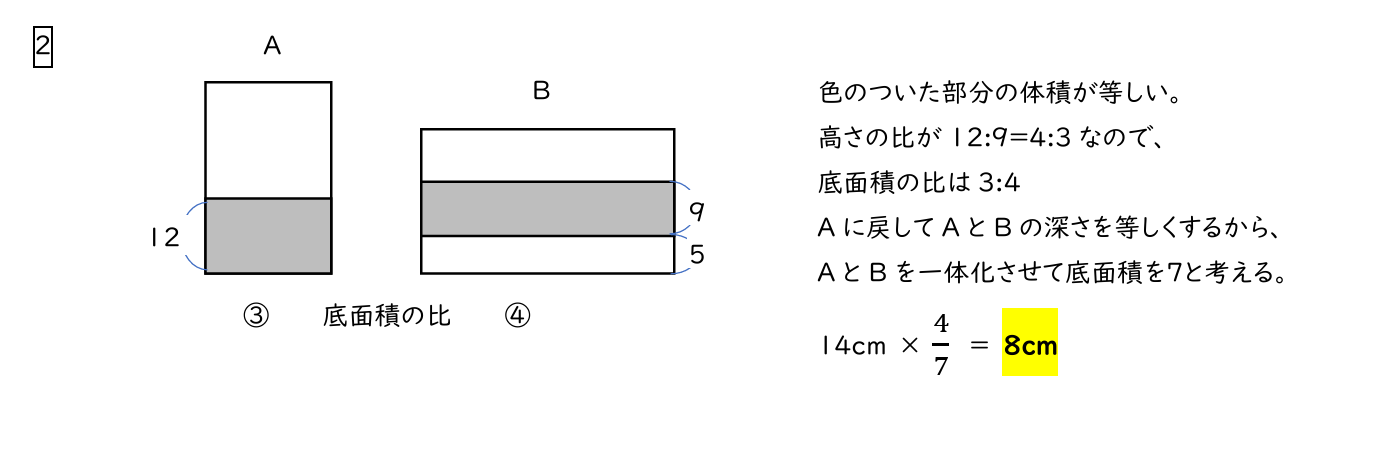
底面積の比が3:4であり、底面積を7にするところまでは分かったのですが、そこからの解説が意味不明です。
4/7の4は何処から出てきたのでしょうか?
また、これから過去問を解いていく中でわからない問題に遭遇することがしょっちゅうあると思いますので、そのときにはどうか質問に答えてくださるとうれしいです。

回答
打方 佑弥 さん、こんばんは。
それはおめでとうございます。がんばってください!!福井県ではユニークなことをしているのですね。
さて、今、底面積が4の割合の水槽Bに全部の水が入っていて高さが14cmですね。高さが同じになるようにした結果は、2つの容器をくっつけて1つにしてしまってすべての水を入れた状態と同じだと考えています。ですから、底面積は $\dfrac{7}{4}$倍になるので、高さはその逆数 $\dfrac{4}{7}$倍になるというのがその式です。
水に関してBの容器でもくっつけた容器でも体積は変わらないので底面積×高さは同じです。くっつけた容器をCとすれば
(Bの底面積)×14cm=(Cの底面積)×(求めようとしている高さ)ですから、
(求めようとしている高さ)=(Bの底面積)×14cm÷(Cの底面積)=14×$\dfrac{(Bの底面積)}{(Cの底面積)}$=14× $\dfrac{4}{7}$
というわけですね。
これで大丈夫ですか?
「さて、今、~その式です。」までが1つ目の解き方、「水に関して~というわけですね。」までが2つ目の解き方という認識でよろしいのでしょうか?
はい、そんな感じです。上のやつをもっと丁寧に説明したのが下のやつです。
底面積の比が 3:4 同じ深さにするには 体積比を 3:4 にすればよい つまり 全体の3/7をAに戻すので Bに残るのは全体の4/7 よってBの深さは 14×4/7=8 Yahoo知恵袋で同じように質問したら、このように返されました。 だいたいは分かるのですが、最後の「Bに残るのは全体の4/7 よってBの深さは 14×4/7=8」という部分。4/7というのは体積比であって高さの比ではありませんよね。なぜ14×4/7=8という式になるのでしょうか。
Bについて考えるから、底面積が変わらないから、体積の比は高さの比になりますよ。
同時に複数の場所で質問してるのですか。ま、気持ちは分からなくはないけど、ちょっとなあ。どっちかに聞いて、回答が出なければ他のところに聞くのが礼儀のような気もしますよ。そうしないと何人もの手を煩わせることになり、無駄になってしまう回答者も出るわけですから。今の場合も、ヤフーの方に聞き直したらよかったのに。
すみませんでした。礼儀がかけていましたね。
これからはどっちか1つに絞って質問します。すみませんでした。
ま、いいのですが、ほかでも聞いているっていうことは内緒にしておきましょうね!