標準偏差

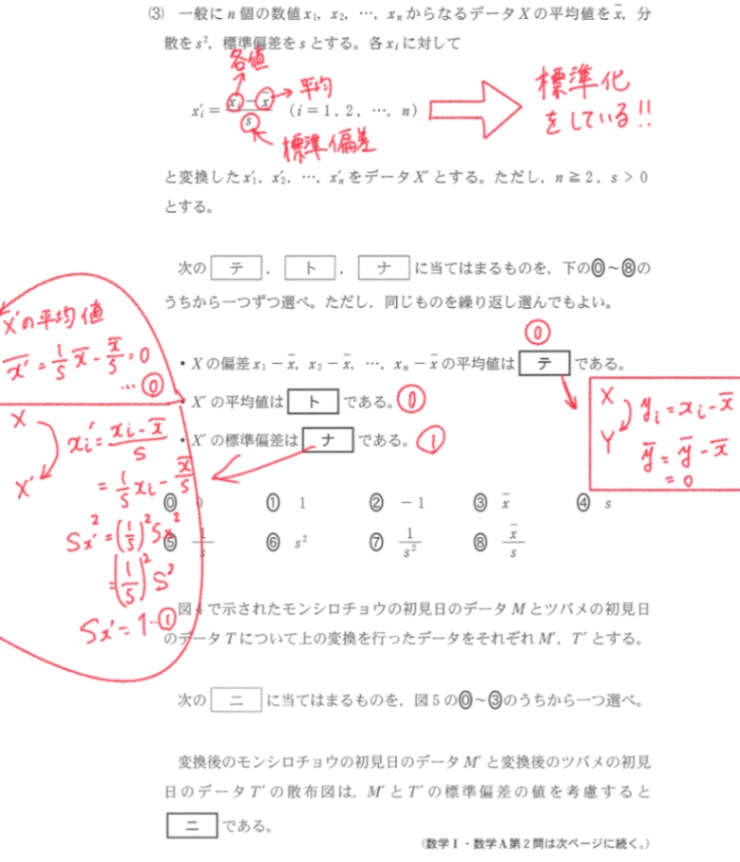
解説講義を見たのですが、どうして『テ』『ト』0になり、『ナ』が1になるのかわかりません。特に教えてもらいたいのは画像4枚目（解説講義です）の青緑で書かれた３つの矢印のところです。式の繋がりを教えていただきたいです

忠 さん、 それらは見ているだけではわからないときは、実際に計算すれば自然に出てきますよ。 青い矢印について。 $y_i$ の平均 $\bar{y}$ を定義通りちゃんと求めてみて。分子が長くなるけれどそれほど大変ではないよ。 $\bar{x'}$ も式は大変かもしれないけれど定義通り計算してみて。 一度ちゃんと計算してみれば、納得できて自然に使えるようになりますよ。 x'は標準化されたものなんだから当然分散は１です。だからそのような式を作らなくても１なのですが、 その$s_{x}$ も $s$ ももともとのデータ $x_i$ の標準偏差のことではないのでしょうか？同じものでは？ 計算がうまくできないようなら、コメント欄で言ってください。 あなたは数Ｂの数列は終わっていますか？シグマ $\sum$ で説明しても大丈夫？ =================================== 追記　2025/07/17　21:15～ じゃ、シグマ使います。 たとえば $\bar{y}=\dfrac{\sum_{i=1}^n y_i}{n}$ $=\dfrac{\sum_{i=1}^n (x_i-\bar{x})}{n}$ $=\dfrac{\sum_{i=1}^n x_i}{n} -\dfrac{\sum_{i=1}^n \bar{x}}{n}$ ここで $\dfrac{\sum_{i=1}^n x_i}{n} =\bar{x} ,\dfrac{\sum_{i=1}^n \bar{x}}{n}=\bar{x}$ だから $=\bar{x}-\bar{x}=0$ となりますよ。 同じように $\bar{x'}$ もできます。 やってみて。