このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
三角不等式
問題の解答教えて頂きたいです!あと、tanの時ってどうやって解くのか教えてほしいです!
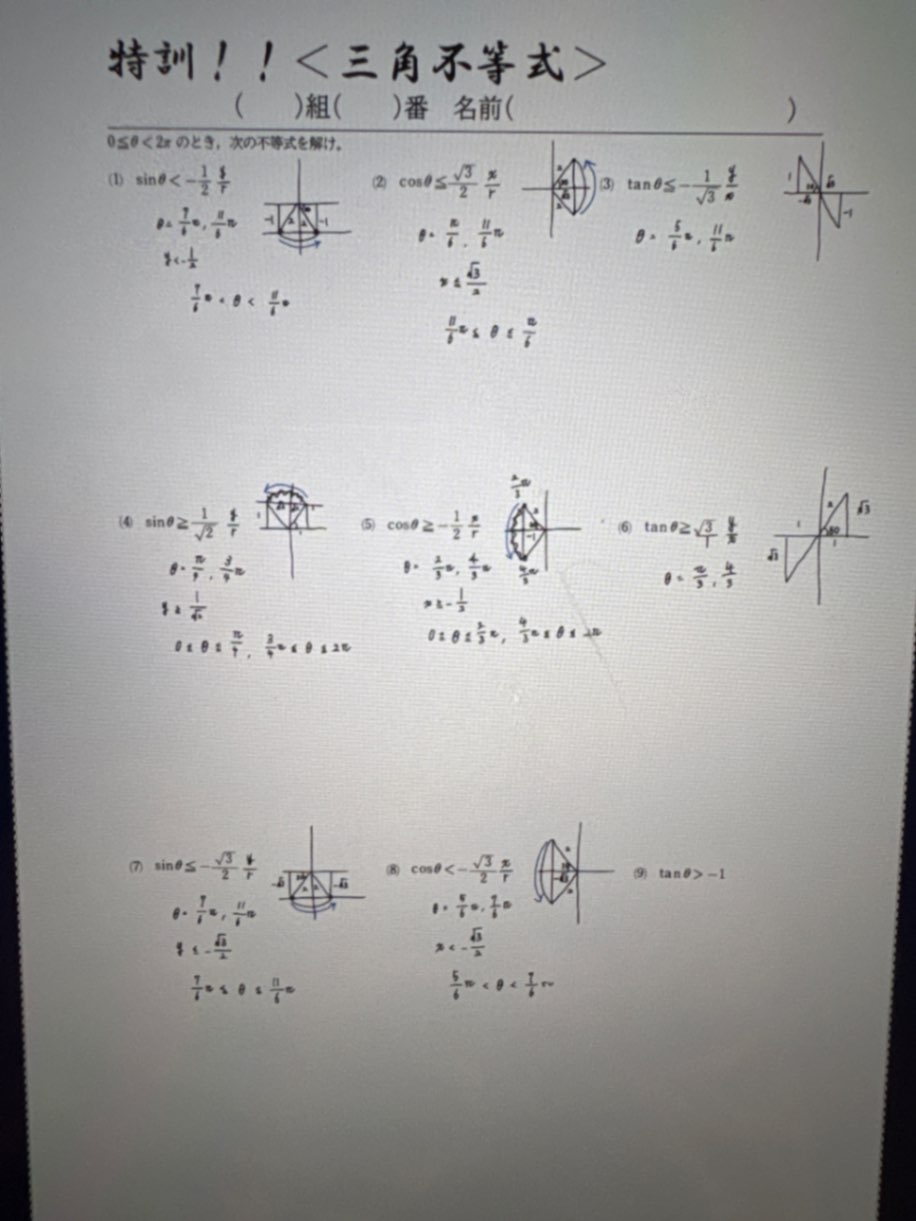
回答
美波 さん、こんにちは。初めての方ですね。よろしく。
まず、答え合わせ。
(1)正解!
(2)間違い…
その図は正しいのですが、角の読み取りで間違えています。
その範囲は「$0\leqq \theta \leqq\dfrac{\pi}{6}$ 」と「$\dfrac{11}{6}\pi\leqq \theta <2\pi$」と読みますよ。
角は小さいほうから始まって、動径は左回りに動きます。その方向で範囲を読みますよ。
(4)間違い
図は正しいです。読む範囲は、あなたの図でゴニョゴニョってなっているところがサインが $\dfrac{1}{\sqrt{2}}$ より大きいところですから、$\dfrac{\pi}{4}\leqq \theta \leqq \dfrac{3}{4}\pi$ と読み取りますよ。
(5)間違えてますね。(4)と同じ間違いですね。図は正しいしゴニョゴニョ部分も正しいのですが、その角の読み取り方が違っていますよ。
$\dfrac{2}{3}\pi \leqq \theta \leqq \dfrac{4}{3}\pi$ となります。あなたの図に書いてある矢印を読み取ればいいのですよ。わかりますか?
(7)残念ながら間違いです。今度は角の大きさ自体が間違ってます。範囲の書き方はそれでいいのですが。
角は $\dfrac{4}{3}\pi$ と $\dfrac{5}{3}\pi$ ですよ。不等式の解はその間ということです。
(8)残念!これも角の読み間違いです。$\dfrac{2}{3}\pi$ と $\dfrac{4}{3}\pi$ ですね。
気になるのは、図に書いてある斜めの線がみんな同じような傾きになっていて、これでは図から角が読みにくいですね。3分のπなのか6分のπなのかがはっきりしないです。1や1/2や√3/2などの大体の値がどのくらいなのか考えてなるべく正しい大きさで三角形を書けば間違いにくいです。また、できれば単位円で考えた方が間違いにくいです。もう三角比の拡張がすんでいるのですから単位円を使いましょう。
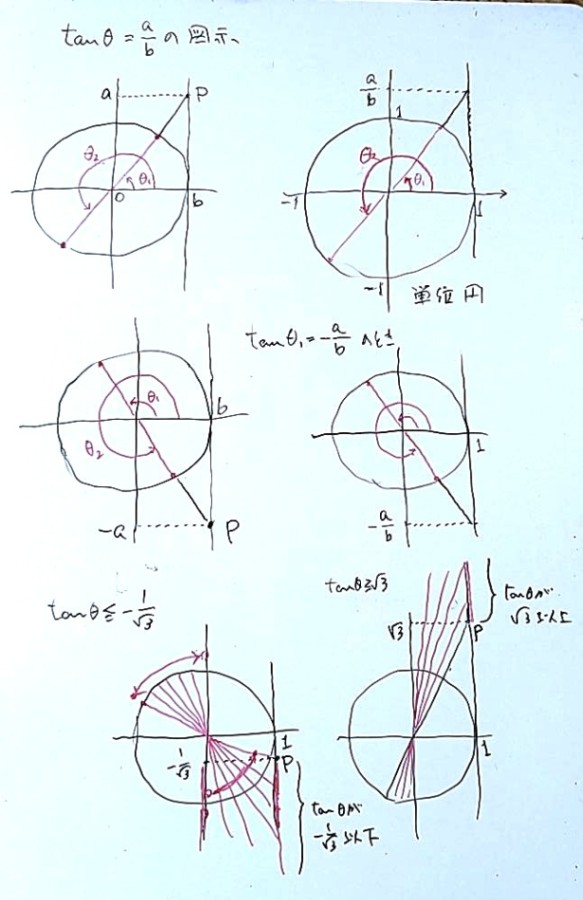
最後に、タンジェントのときの解き方ですが、先生によって多少違うと思います。授業でしっかり聞いてください。
私は単位円を書いて直線x=1の上にタンジェントが現れるので、それを使って教えていましたよ。
図を添付しますのでながめてください。これだけでは分かりにくいと思いますので、まずサインコサインの不等式についてやり直して、納得できてからタンジェントの話をしたいと思います。
サインコサインの問題が納得できたら、コメント欄に連絡ください。いっぺんに説明を書くより、少しずつ進みましょう。
これで大丈夫ですか?ここでは会話型を目指しています。これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。返事がないと、せっかく書いたものを読んでくれたのかどうか、書いたものが役に立ったのかどうか、こちらではわからないのです。コメントよろしく。