このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
4次関数の最大、最小
写真の問題についてです。
下部の注意書きの式をどの様にまとめたら
7^3/16(7-12+4)
になるのかが分かりません。
解説お願い致します。
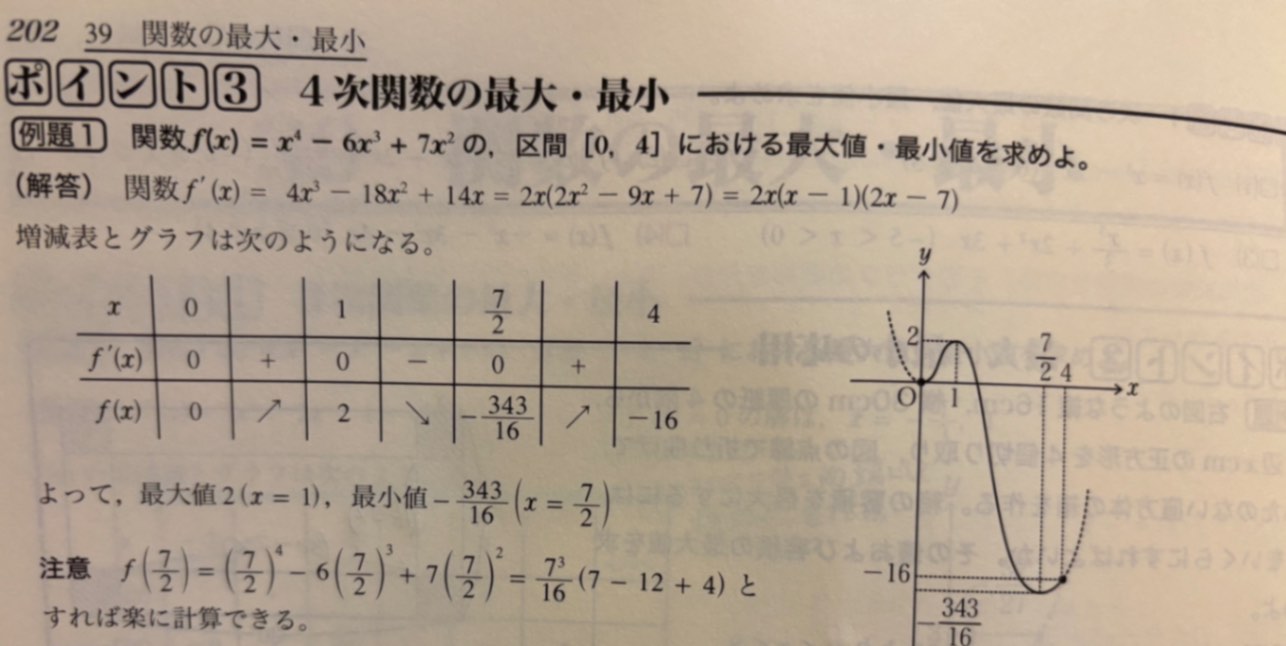
回答
ひなたさん、こんにちは。ちょっと久しぶりでしたね。
分数の累乗の足し算はいやだったので、分子の7の最小次、分母の2の最高次を調べました。
7の最小次数は3、2の最大次数は4でしたので $\dfrac{7^3}{2^4}$ を共通因数としてくくりだします。なぜそんなことをするかというと、それをくくりだすと、残りが全部整数になってくれるからです。
$\left(\dfrac{7}{2}\right)^4=\left(\dfrac{7^3}{2^4}\right)\times 7$
$6\left(\dfrac{7}{2}\right)^3=6\left(\dfrac{7^3}{2^4}\right)\times 2$
$7\left(\dfrac{7}{2}\right)^2=\left(\dfrac{7^3}{2^4}\right)\times 2^2$
これで大丈夫ですか?まだ計算方式に疑問が残るなら、コメント欄になにか返事を書いてください。あ、分かった場合もなにか書いてくれるとうれしいです。
こんにちは。 返信遅くなりました🙇 下二つの項は分母を4乗で合わせて括り出しているので足りない分を2を掛けて辻褄を合わせているという事なのですね。 納得できました。 今回も回答ありがとうございました。
どういたしまして。ちょっとした計算のテクニックですね。それほど重要なことではないです。あまり気にしないように!では、またどうぞ。