このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
極値を持つか否かの確認
黄色いマーカーのところです。
なぜa≦0の時に極値を持たないと言えるのか教えていただきたいです。また、4枚目の問題では極値が存在するかの確認をされていませんが、なぜでしょうか?
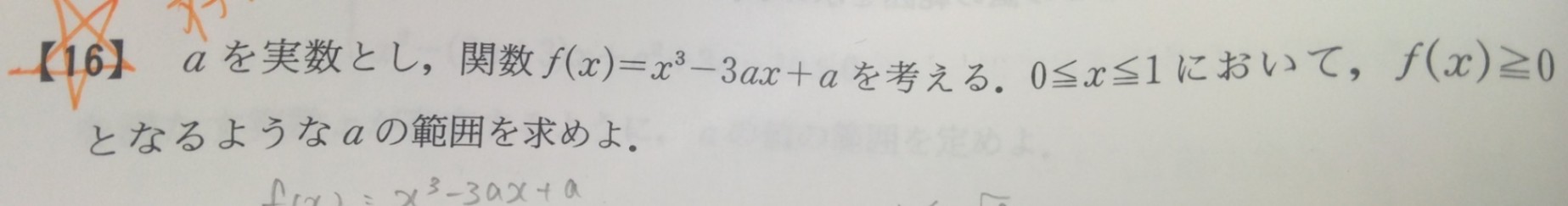
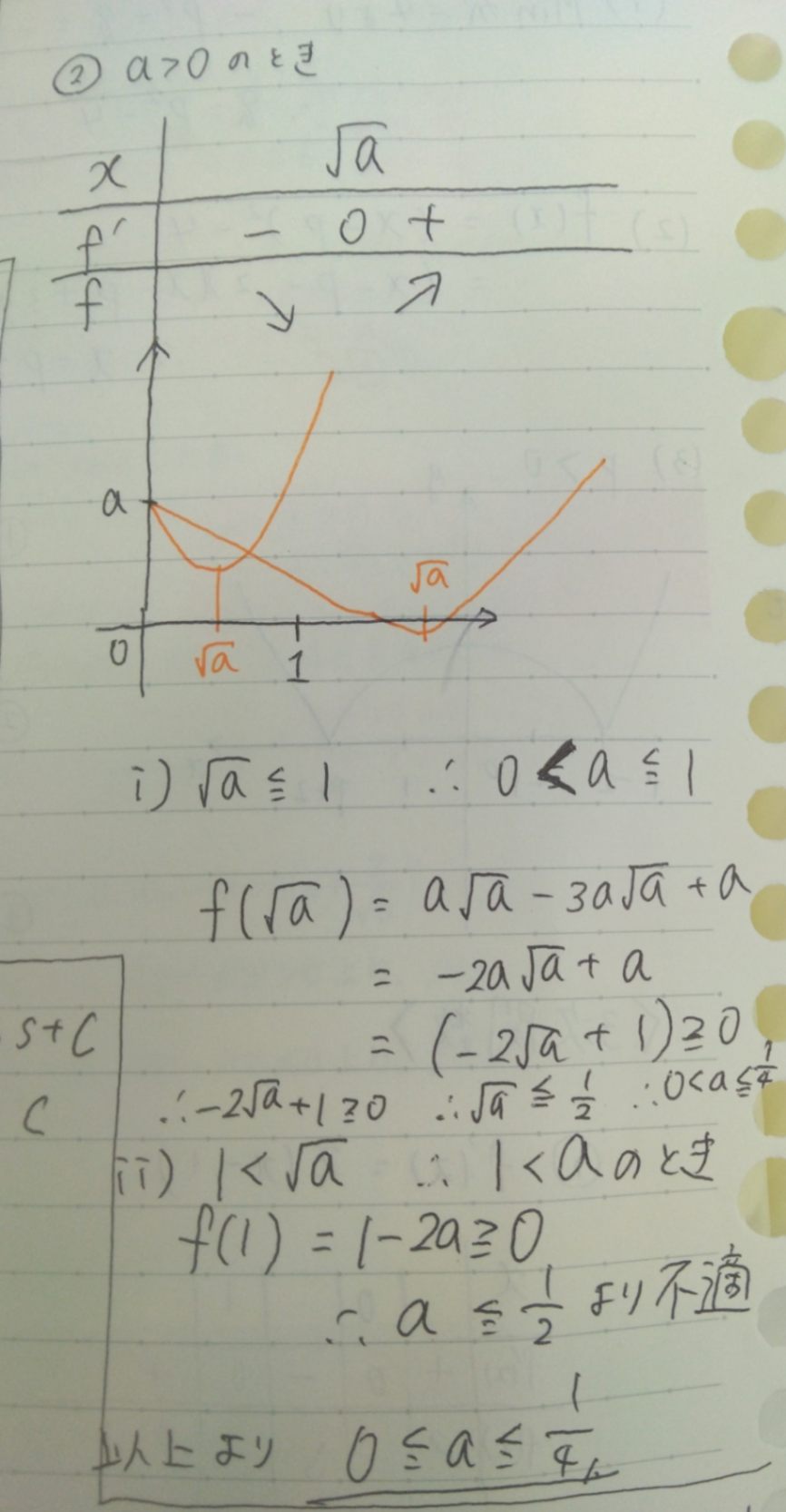

回答
忠さん、こんにちは。いやぁ、暑いですね!
さて、極値はf'(x)=0となるようなxで取ります(必要条件ですが)。そして、その前後でf'(x)の符号が変わります(前のと合わせて必要十分条件)。
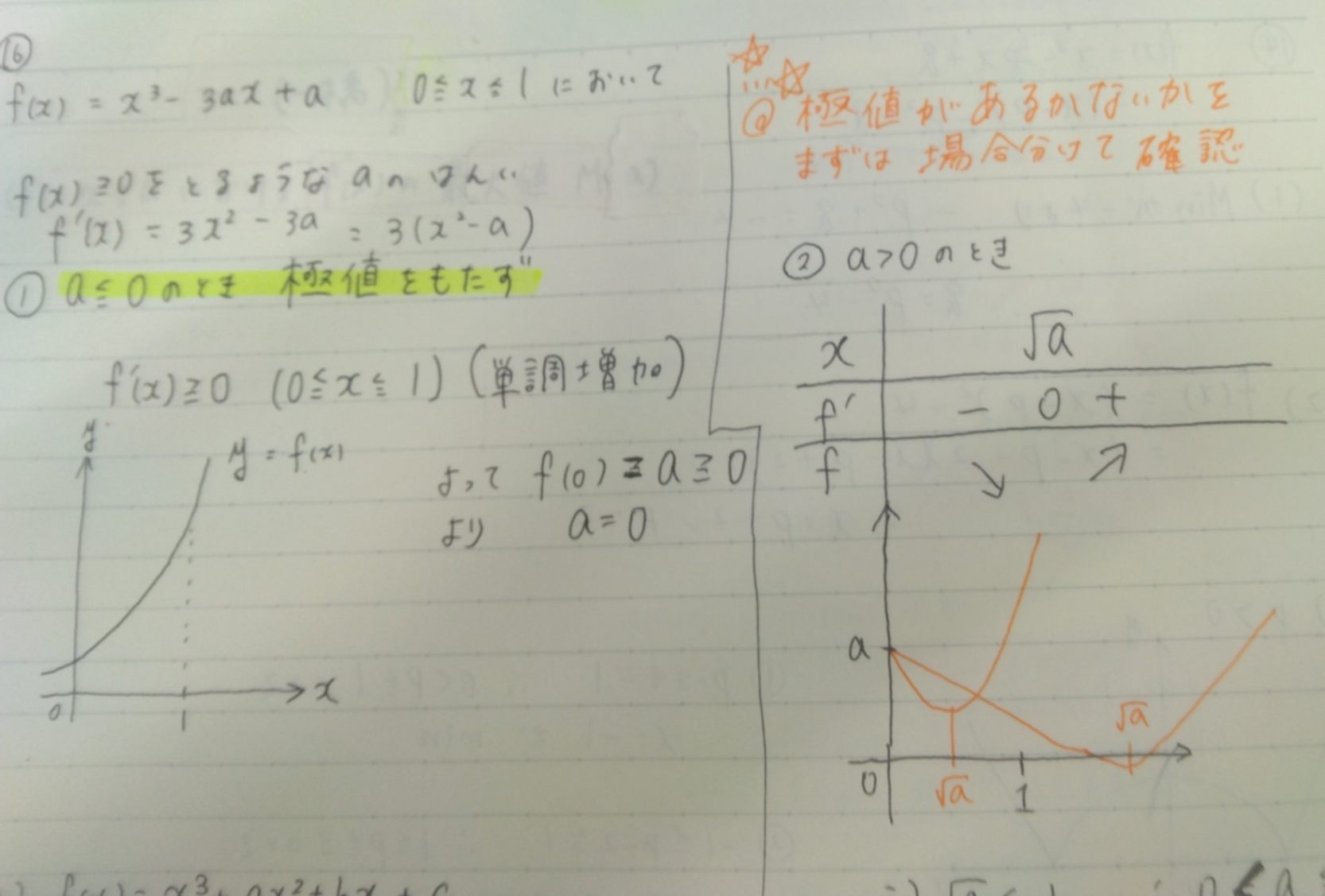
a=0のときはf'(x)=3ⅹ²で、x=0でf'(x)=0となりますが、x=0の前後で符号が変わらず、x=0では極値になりません。
a<0の時はx²-aは常に正になり、f'(x)=0となるようなxは存在せず、極値はないです。
以上より「a≦0のときは極値はない」と分かりますよ。
a>0のときはf'(x)=0となるようなxが存在し、その前後で符号が変わるので極値があります(2つ)。
4枚目の問題は、aではなくa²ですので、a=0の時は極値を持ちませんが、それ以外の時はx=±aで極値を持ちます。この問題のaは0にはなりませんので、a>0という設定では常に極値を持つので場合分けはしていませんよ。初めの問題のa>0は、この問題のa²>0に対応します。a≠0のときはa²>0です。だから0<a…となっていて、等号はついていません。ま、問題にa>0とあるので当然と言えば当然ですが。
これで大丈夫ですか?
そういうことだったんですね…!!!納得しました!!!ありがとうこざいました!!
お役に立ったのならよかったです。