このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
不定積分の分野
(3)の解説なんですが、Pの部分がよく分かりません(;;)
①Pが急に出てたこと←最初、数列で処理しようかと思ったけど無理でした。最終的に∑で表されているのでその方法での解き方があれば教えて頂きたいです。
②Pの発想が分かりません。なんで1,n,n-1,の順番でPが使われたのか(´・_・`)
お願いします( .ˬ.)"

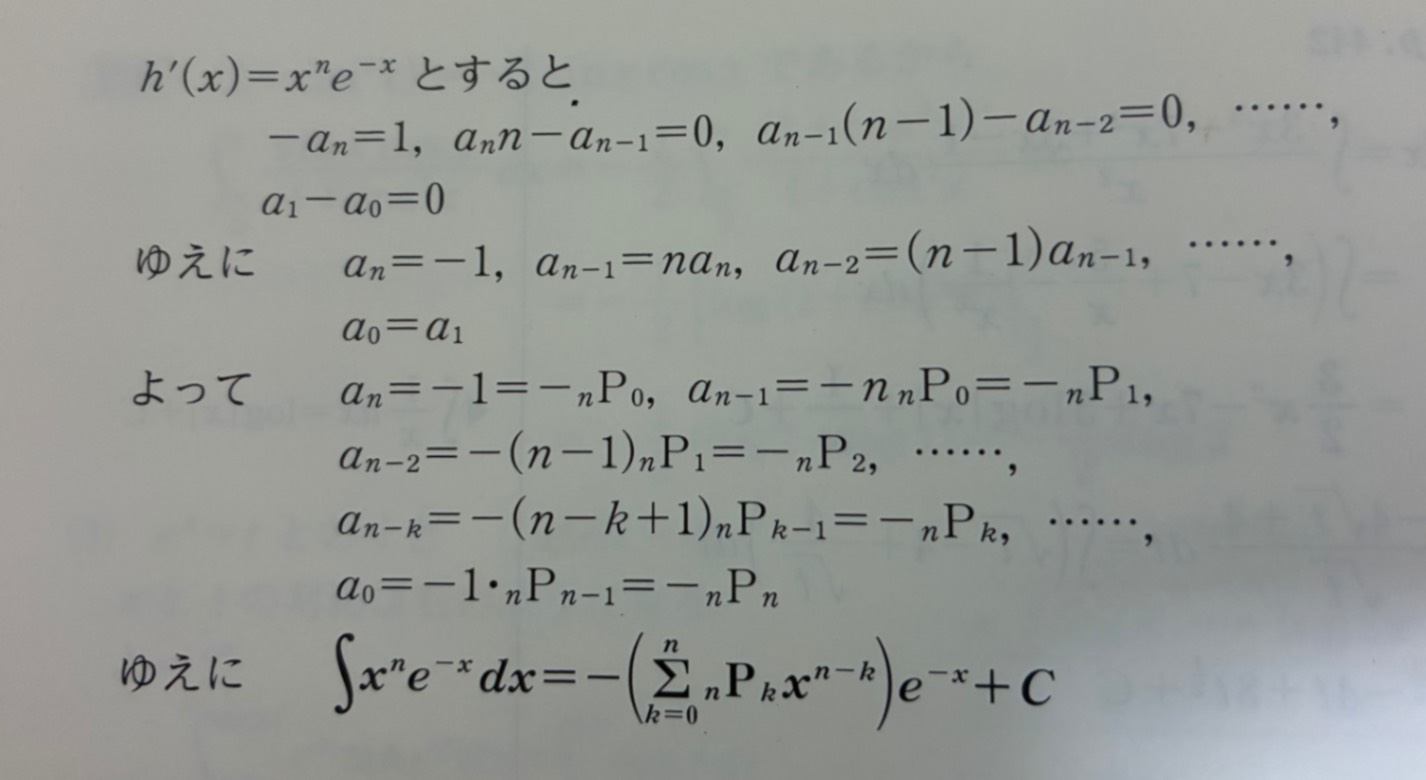
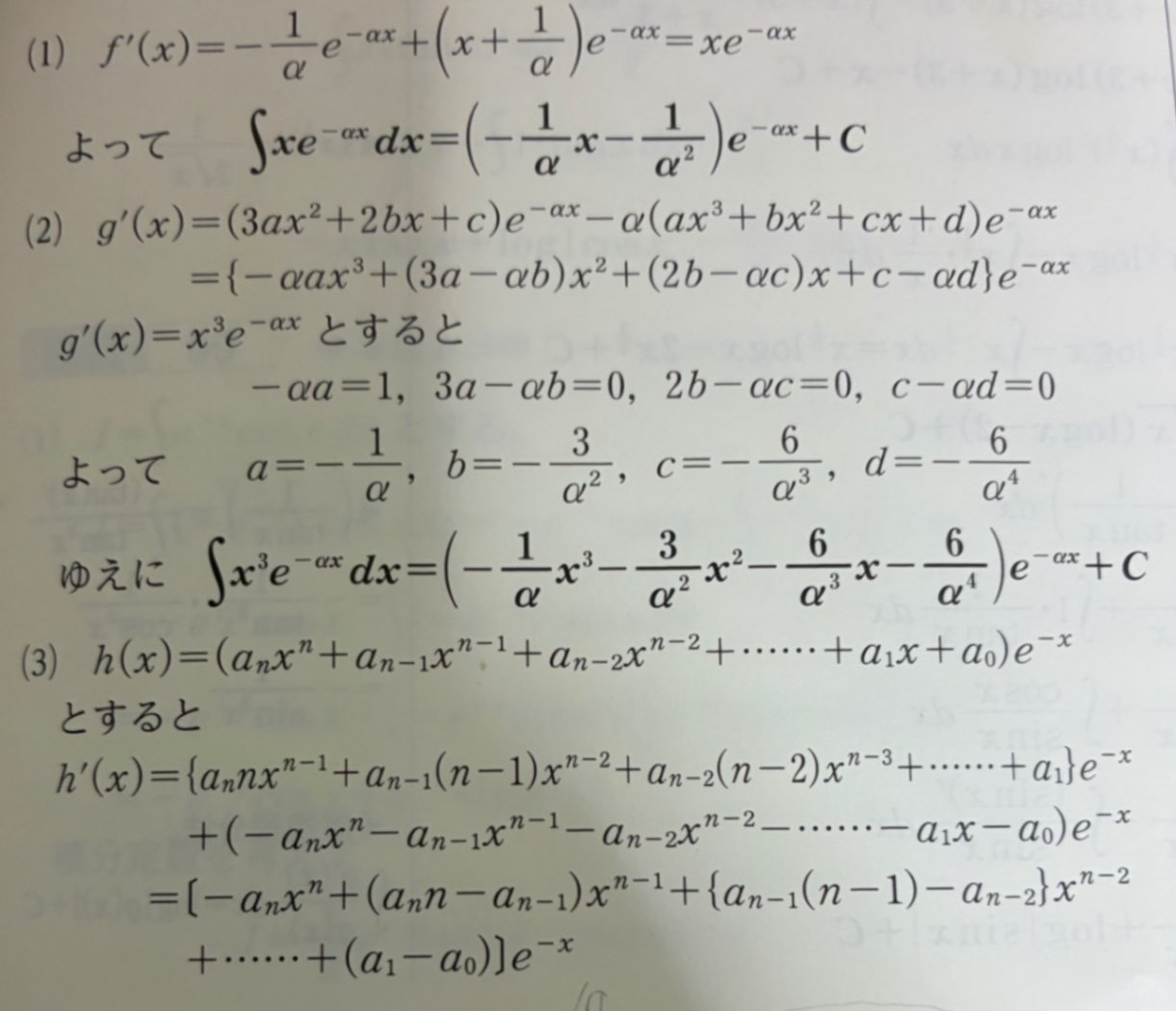
回答
い あ さん、こんばんは。初めての方ですね。よろしく。
「1,n,n-1の順番」は間違いですね。「n,n-1,n-2の順番」になっていますよ。
なるほど、これだけ見ると、なぜPが出てきたか分からないですよね。なんでそんな発想ができるんかい!という感じです。
でも、2枚目の写真の「ゆえに」のあとをもう少し頑張って書いてみればその発想が出てきます。
$a_n=-1$
$a_{n-1}=na_n=-n$
$a_{n-2}=(n-1)a_{n-1}=-n(n-1)$
$a_{n-3}=(n-2)a_{n-2}=-n(n-1)(n-2)$
$a_{n-4}=(n-3)a_{n-3}=-n(n-1)(n-2)(n-3)$
$a_{n-5}=(n-4)a_{n-4}=-n(n-1)(n-2)(n-3)(n-4)$
…
…
このように書いていけば、Pを使うときれいに書けるかも、という考えも出てきます!
$a_{n-4}=-_nP_4,a_{n-5}=-_nP_5$ などが思いつけば、
無理やり $a_n=-1=-_nP_0$ と書けばいいな、とも思えますよ。
ま、かなり頭を柔らかくしていないとできない考えかもしれません。そういう意味では難しい問題です。
Pの発想が出てこなければ、Pの代わりに $\sum_{r=0}^n \dfrac{n!}{(n-r)!}x^{n-r}$ と書いてもいいですね。
これで大丈夫ですか?
ここでは会話型を目指しています。
これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。返事がないと、せっかく書いたものを読んでくれたのかどうか、書いたものが役に立ったのかどうか、こちらではわからないのです。コメントよろしく。
n,n-1,n-2の順番なんですね!aのnから0までの数列としか見れていなかったのは反省点です、、 わかりやすい説明ありがとうございます! これからも質問することがあると思うのでよろしくお願いします(*^^*)
お役に立ったのならよかったです。またどうぞ!