中学校　空間図形

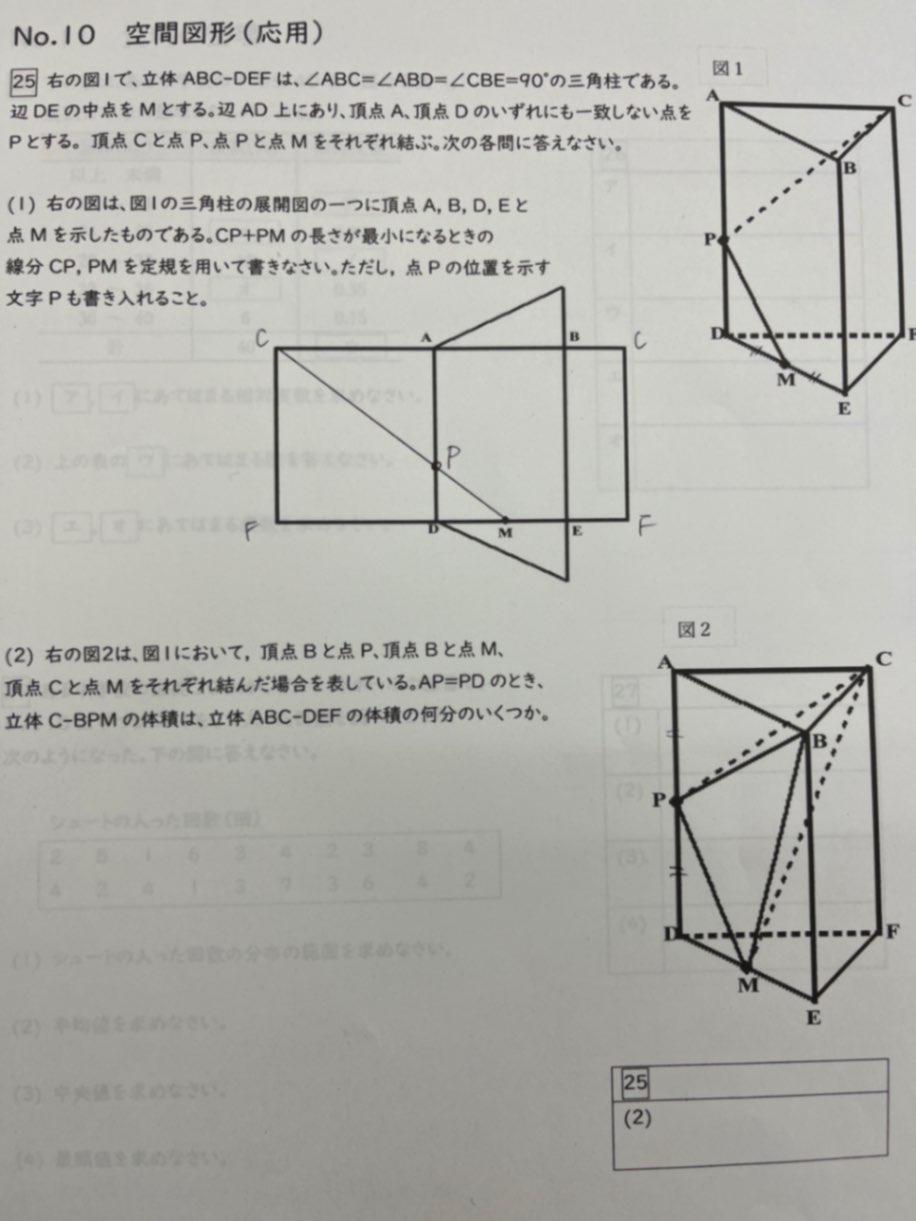
（２）が分かりません。 よろしくお願いします。

近藤 菜摘 さん、こんにちは。初めての方ですね。よろしく。 あれ？問題文の1行目に間違いがありますね。∠ABDではなく∠ABE=９０°ですね。 ここは質問箱なので、丸投げはちょっと…なのです。 できればあなたが考えたところまでを知りたいですね。具体的にどこから解説すればいいのかわからないからです。 そういうわけで、まずはヒントというか方針を書きます。決していじわるで解答を書かないわけではありません。やはり自分で考えて解くのが力になると思うのです。 底面DEFは直角三角形です。そこでそれと合同な三角形FGQをくっつけて長方形を作ります。わかりますか？Qは新しくくっつけた三角形の直角の頂点です。 この長方形QDEFを底面とした四角柱をもとに考えます。上底にも△ABCに合同な三角形がくっつきますよ。 もとの三角柱ABC-DEFの体積をVとすると、この四角柱の体積は２Vです。 さて、ここからは見方を変えますよ。この四角柱（直方体）を底面が長方形ADEBである四角柱と考えます。 すると四角錘C-ADEBの体積は元の四角柱の1/3ですね。よって四角錘C-ADEBの体積は2/3Vです。わかりますか？ この四角錘と、求める三角錐C-PMBは高さが同じです。だから底面積の比が体積の比になります。 さて、△BPMは四角形ADEBの面積の何分のいくつでしょうか？ これが分かればなんとかなるのですが、どうでしょうか？ ここまでのヒントで少し考えてみてください。 これで大丈夫ですか？ ここでは会話型を目指しています。これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。返事がないと、せっかく書いたものを読んでくれたのかどうか、書いたものが役に立ったのかどうか、こちらではわからないのです。コメント、よろしく。