規則性の問題

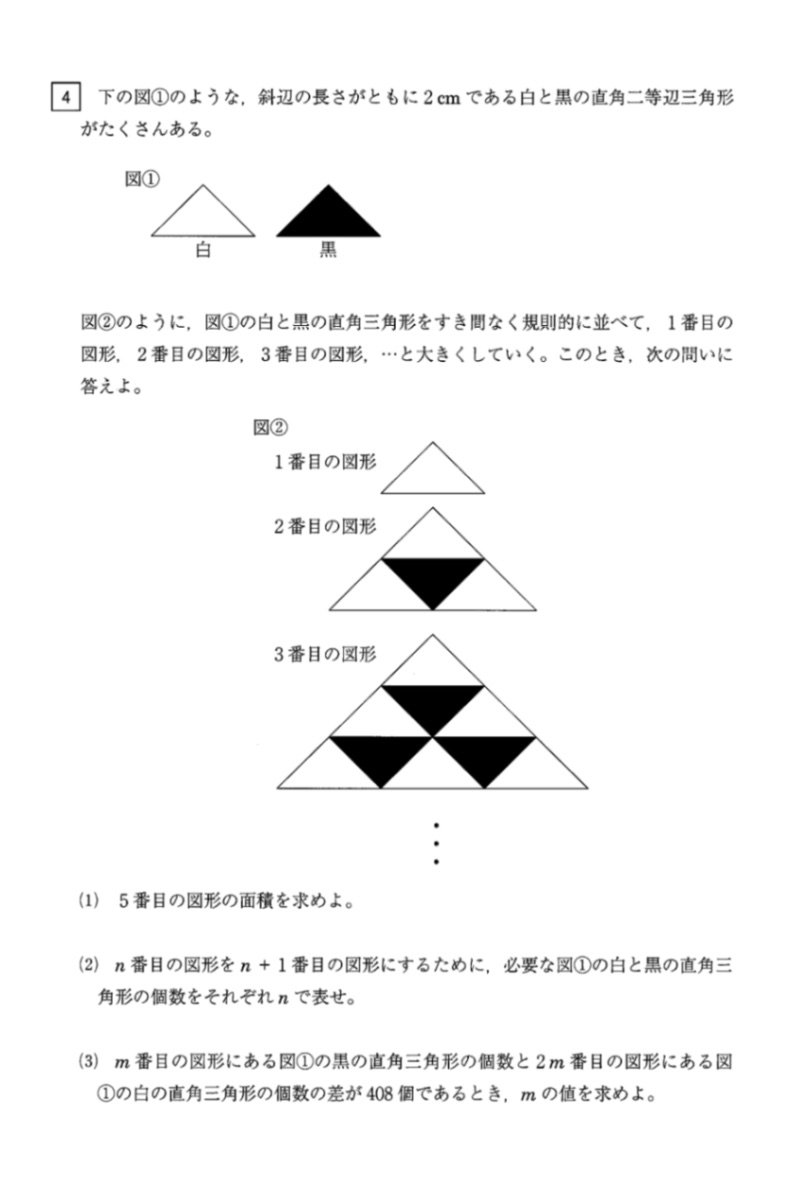
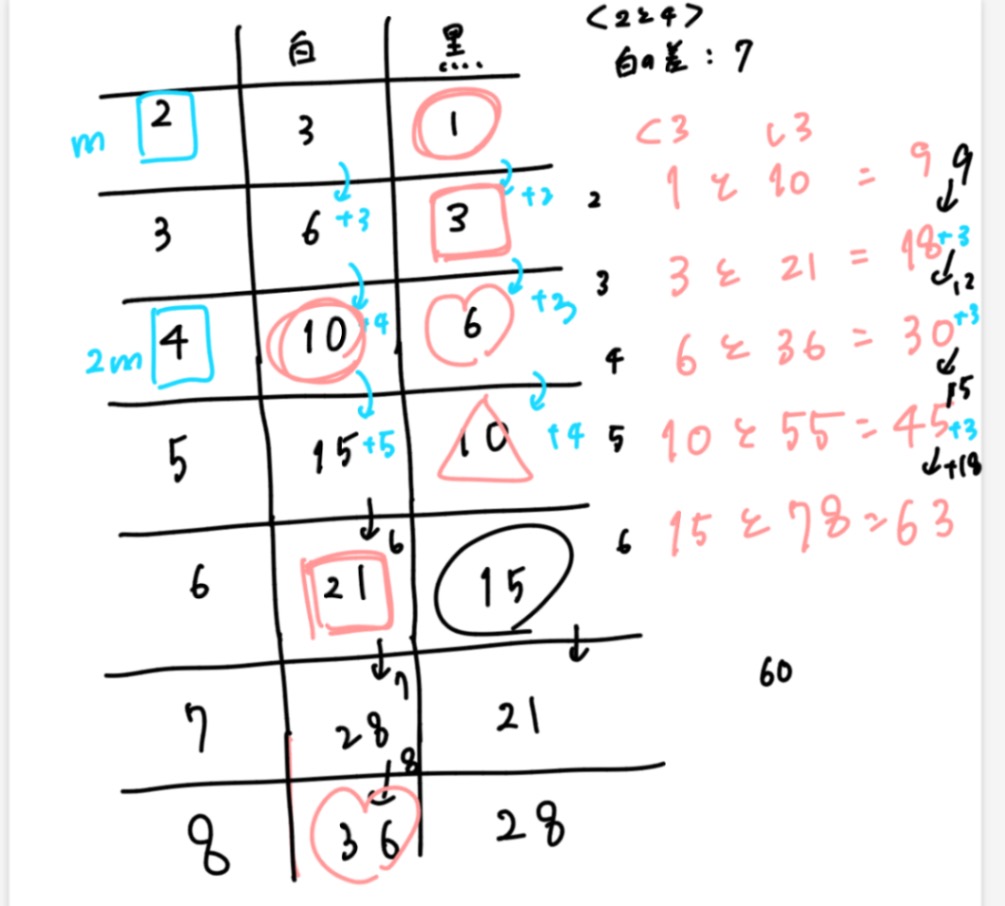
(2)まで解けましたが(3)がどのような法則なのか考えつきません。 mと2mに具体的な数を入れましたが規則が見当たらないです。 今わかっていることは三角形の数は黒、白どちらも＋3からスタートし順に+4、+5..と続くこと。(黒は白よりも一回遅れ) 2と4をmに置き換えると差は9 3と6のときは18 そのあとは30、45、63 です。 白と黒の差は常にmの数にもなります 何かの累乗か倍数の関係かと思いましたが白の三角形が3の倍数というわけでもありませんでした。 考える過程のヒントが欲しいです。 よろしくお願い致します。

ゆ ゆ さん、こんにちは。２回目、いらっしゃい！ 回答する前に知りたいことがあります。 あなたは中学生ですか、高校生ですか？何年生ですか？ それによって説明が変わりますので。 中学生だとしたら、２次方程式は分かりますか？ また、 $1+2+3+\cdots +n=\dfrac{n(n+1)}{2}$ で計算できることは知っていますか？ これは１９世紀の数学者ガウスが、少年の時に見つけた計算方法として有名なのですが、その話は知っていますか？ それと、これは何の問題ですか？問題集？模擬試験？よく公立高校の入試に出るタイプですが。それとも数列の練習問題？ 解説は持っていないのですね。 お返事、お待ちしています。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ コメント、拝見しました。 高校入試問題ですね。 そうなると、ぜひその計算法は知っていてほしいです。 １から４までの和は１０ですが、それは $\dfrac{4\times 5}{2}=10$ で求まります。 １から１０までの和は５５ですが、それは $\dfrac{10\times 11}{2}=55$ で求まります。 １から１２００までの和はとても足し算では大変ですが、 $\dfrac{1200\times 1201}{2}=600\times 1201=720600$ で求まります。 なぜこの方法で計算できるのかは、下のURLに行ってみてください。難しい理屈ではありません。 https://math.nakaken88.com/textbook/master-sum-of-n-and-quadrangle/#n%E3%81%BE%E3%81%A7%E3%81%AE%E5%92%8C%E3%81%A8%E9%95%B7%E6%96%B9%E5%BD%A2 や、 https://math.nakaken88.com/textbook/basic-sum-of-n/ など。これはなんのことわりもなく使っていい公式です。 たぶんこれを使うのが速いし楽だと思います。 ①ｍ番目の黒の個数＝$1+2+3+\cdots +(m-1)$ これは計算法のｎがm-1のばあいですから、 $1+2+3+\cdots +(m-1)=\dfrac{(m-1)(m-1+1)}{2}=\dfrac{(m-1)m}{2}$ となります。 ②２ｍ番目の白の個数＝$1+2+3+\cdots +2m$ これは計算法のｎが２ｍの場合ですから $1+2+3+\cdots +2m=\dfrac{2m(2m+1)}{2}=m(2m+1)$ と表せます。 問題より $m(2m+1)-\dfrac{(m-1)m}{2}=408$ となります。 これはｍの2次方程式なので、整理して $m^2+m-272=0$ これは因数分解できます。見てるだけじゃ無理だけど、素因数分解して $-272=-2^4\times 17=-16\times 17$ だから $(m-16)(m+17)=0$ m=16,-17 m>0だからｍ＝１６ ゴメンナサイ、途中経過全部書いてしまいました。 わたしはもう頭が硬いので、このような解法になってしまいます。 ひょっとして、柔らかい頭で考えると、すならしい解法があるのかもしれません。 学校で先生の解説がこれ以外の解法だったら教えてくれるとこちらも勉強になります。お願いしますね。 これで大丈夫ですか？前回のようにコメント欄になにか返事を書いてください。よろしく。 なお、高校に入れば、あなたが3枚目の写真の右の方に書いてある規則性から求めることができるようになります。楽しみですね！！