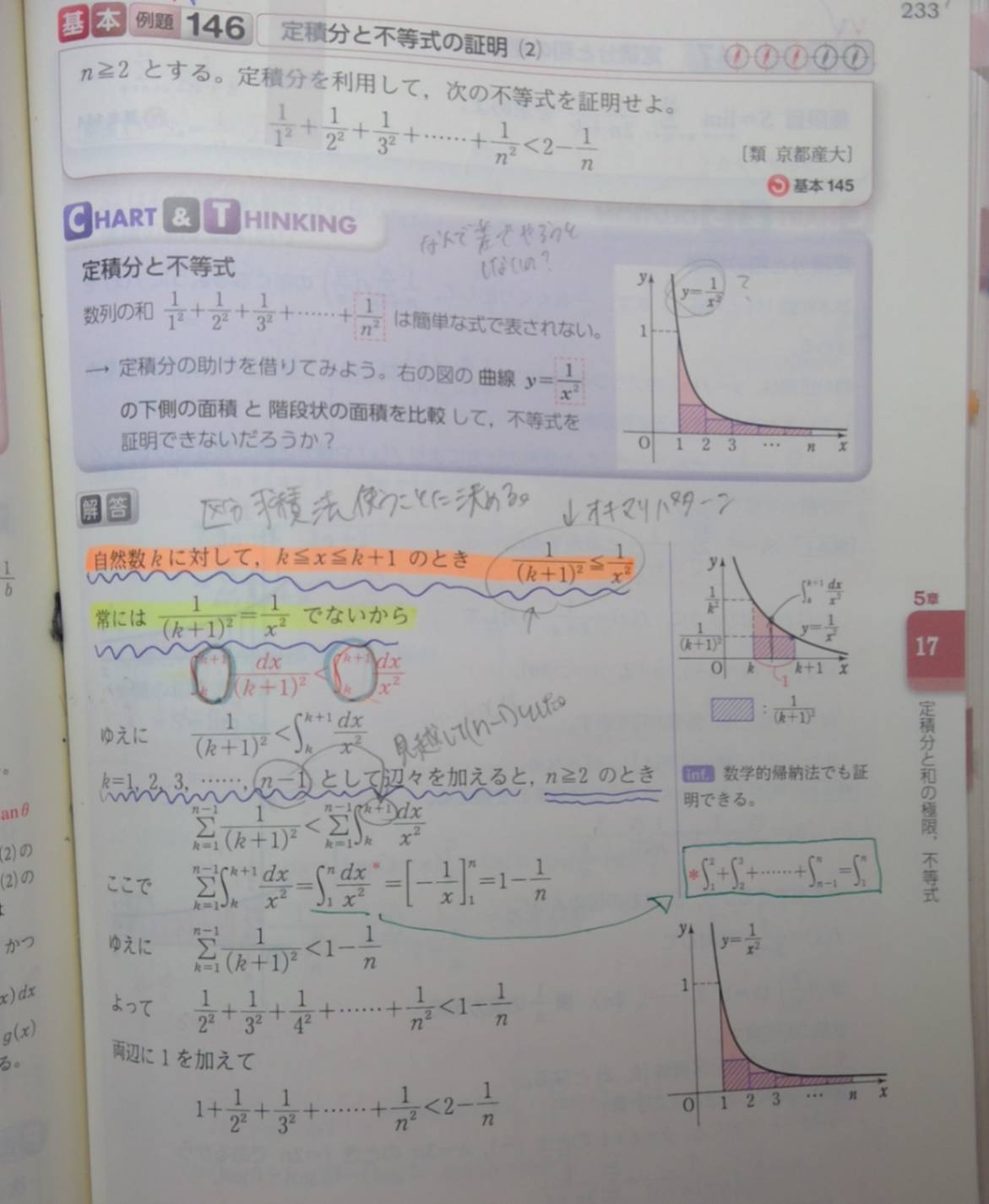
定積分と不等式の証明

解答に最初に自然数kに対して、k<=x<=k+1のとき1/(k+1)<=1/x²とかいてあるけどなんでこうするのですか。逆数にすることはわかるけど、なぜ1/(k+1)<=1/x²だけにするのか。1/k²はどこに行ったのかわからない。めっちゃ丁寧に教えてほしいです。

か な さん、こんにちは。初めての方ですね。よろしく。 まず、区分求積法を利用しようと気が付いたらｋ≦ｘ≦ｋ＋１の範囲で考えるのはいいですか？今からシグマして積分範囲をつなげようという意図があるからです。 つぎに、なぜ $\dfrac{1}{x^2} \leqq \dfrac{1}{k^2}$ のほうは使わなかったのかというと、証明すべき不等式の右辺が積分に由来するらしいことが分かるので、右辺にｘが入るような部分 $\dfrac{1}{(k+1)^2}\leqq \dfrac{1}{x^2}$だけを使うつもりで $\dfrac{1}{x^2} \leqq \dfrac{1}{k^2}$ のほうは無視したのです。 もし問題が「 $1-\dfrac{1}{n}<\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\cdots +\dfrac{1}{n^2}$を証明せよ」だったら、証明すべき不等式の左辺が積分に由来するみたいだと見抜き、ｘが左辺にくる部分の不等式 $\dfrac{1}{x^2} \leqq \dfrac{1}{k^2}$ の方を使いますよ。 これで大丈夫ですか？「めっちゃ丁寧」であるかは心配ですが（笑）。 ここでは会話型を目指しています。これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。返事がないと、せっかく書いたものを読んでくれたのかどうか、書いたものが役に立ったのかどうか、こちらではわからないのです。コメントよろしく。