このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
外心の線分の長さの積
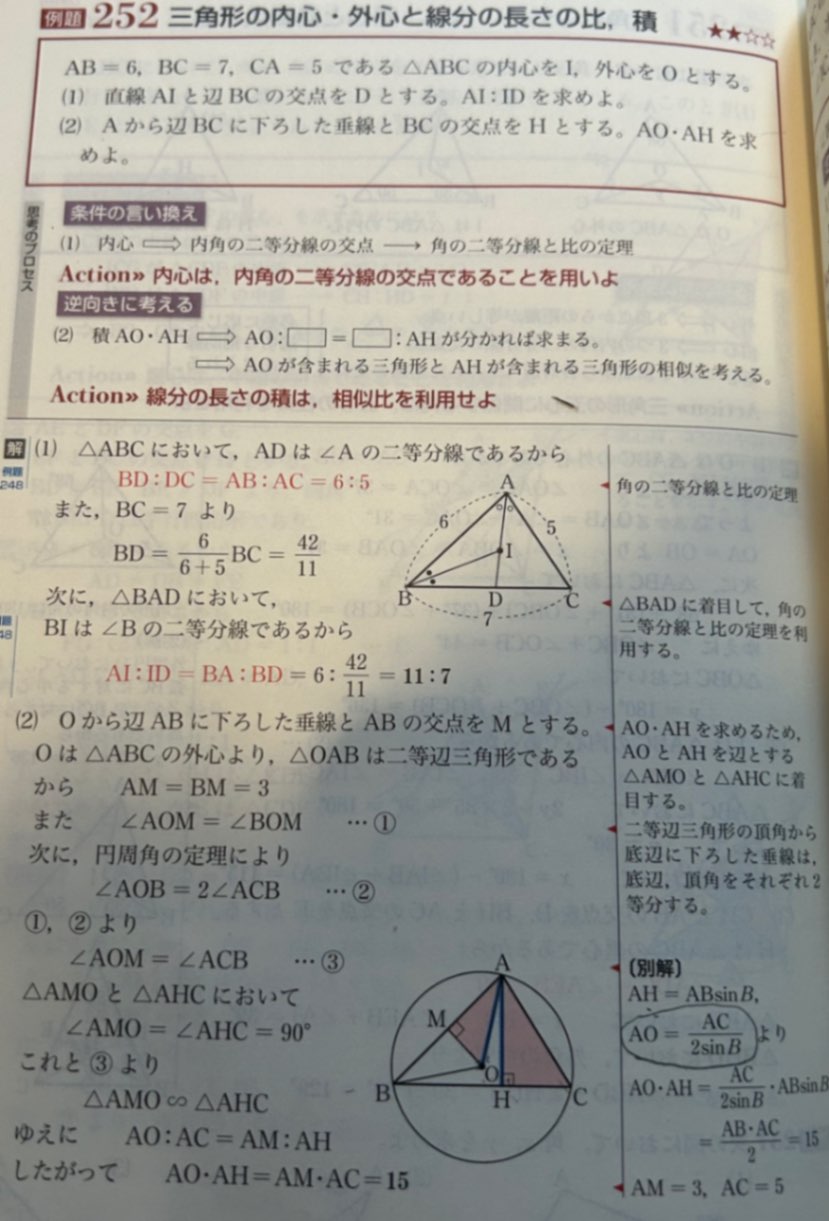
回答
まずOは外心だから三角形OACはOA=OC の二等辺三角形。 つまりOから下ろした垂線はACの垂直二等分線となる。 その交点をKとし、 弧ACから角ABCと角AOCができていて、それらは円周角と中心角の関係であるから、 角AOCは2倍の角ABC Kは線分ACの中点であるから 角AOKは2分の1倍の角AOCだから角Bと同じ。 こんな感じですかね?! 多分理解できたと思います!わかりやすく丁寧な説明ありがとうございます! ところで質問なんですが、Oから ACに垂線を引こう!という発想が出るのでしょうか?それともこれは基礎中の基礎で覚えておくべきことですか?
はい、あなたが書いているように答案を作っていけばいいのです。それでいいです! そうですよね。問題の解答をみると、どうしてそんなことに気が付くのかっていう場合がよくありますよね。 ある意味、経験は役に立ちます。でもすべてを経験することはできないのだから、いろいろ推理してやってみて、だめなら他の方法を考えて…とやっていくしかないです。わたしもあなたの質問個所をみて、なかなか進みませんでしたよ。で、∠Bに関係するもの→中心角 とか、AOに三角比で関係する場所は?など考えていて、直角三角形を作ってみたら大当たりでした!基礎中の基礎なんてものではないです。推理力とか「ダメなら別のやり方で」とか、手を動かし、書いたり書き込んだりの結果として得られます。 がんばってください。 またどうぞ。
丁寧にご回答ありがとうございます! 数学苦手なのでこれからもよろしくお願いします🙇
お役に立ったのならよかったです。こちらこそよろしく。またどうぞ。