このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
数列の和
写真の問題(3)についてです。
解説で書かれているところまでは行けたのですが、その後どのようにまとめれば解に辿り着けるのかが分かりません。
解説お願い致します。
【写真】
1枚目→問題「次の和を求めよ」
2枚目→解答
3枚目→解説
4枚目→追加写真、自身のノート
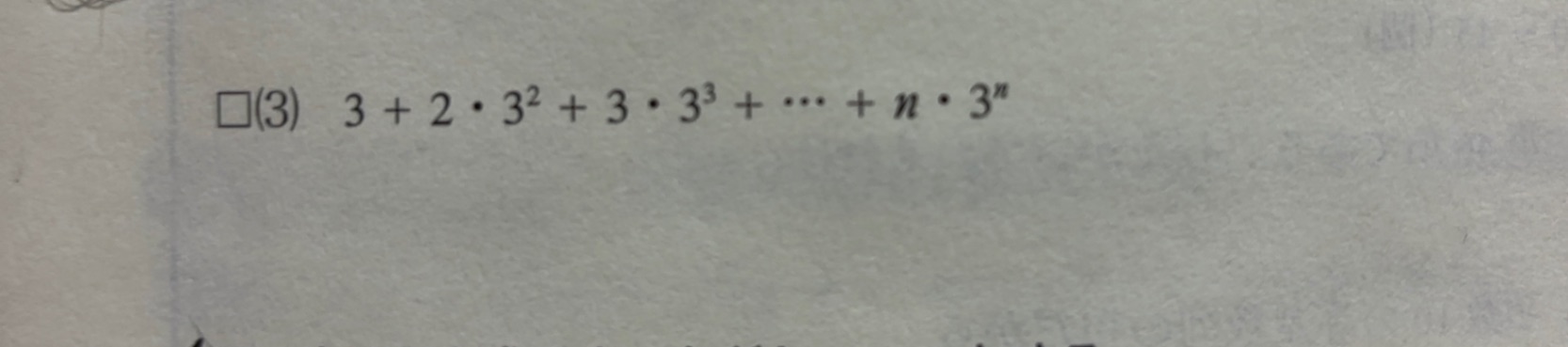
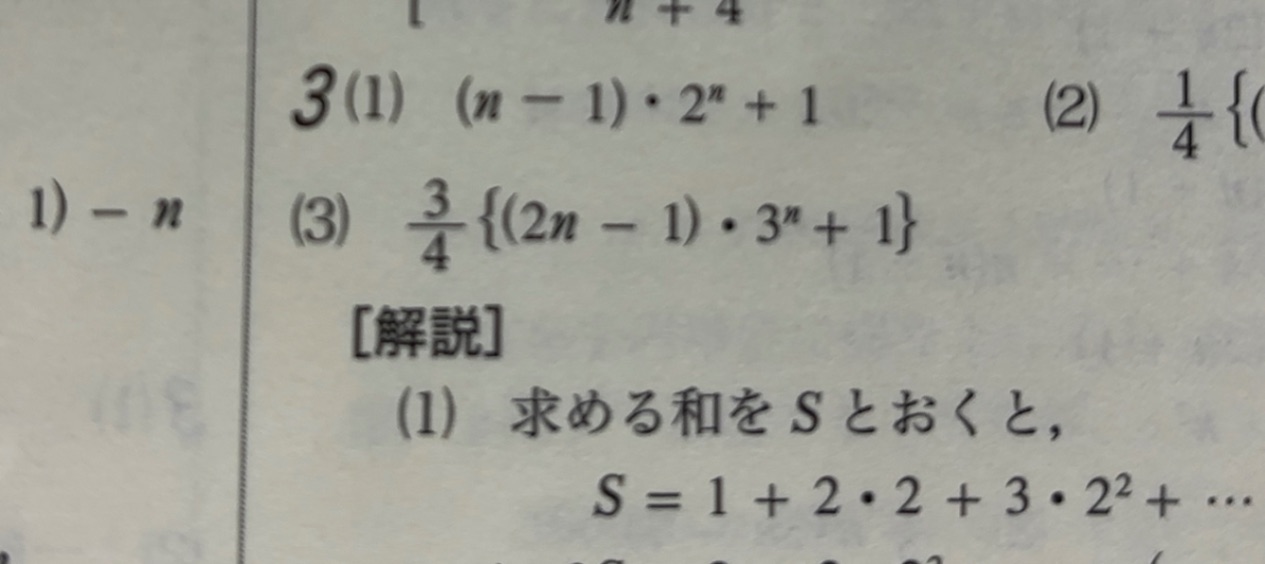
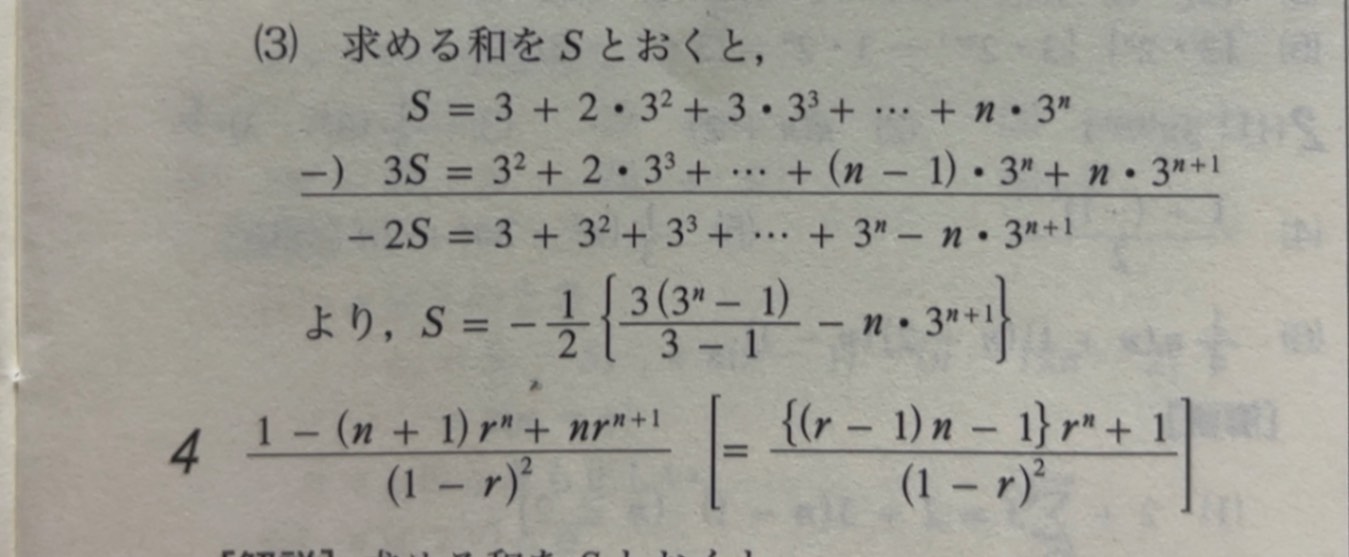

回答
ひなた さん、こんばんは。
この手の最終的な答の式は、なにもこれと同じじゃなくても大丈夫ですよ。
あなたができるだけきれいにまとめた式でも大丈夫かもしれません。
それを見せてくれるといいのですが。
その変形を書いてみます。なかなか自然にはいきません。その答になるように考えていきました。
$S=-\dfrac{1}{2}\left(\dfrac{3(3^n-1)}{2}-3n\cdot 3^n\right)$
$=-\dfrac{3}{4}(3^n-1)+\dfrac{3}{2}n\cdot 3^n$
$=\dfrac{3}{4}(-3^n+1)+\dfrac{3}{4}\cdot 2n\cdot 3^n$
$=\dfrac{3}{4}\left(-3^n+2n\cdot 3^n+1\right)$
$=\dfrac{3}{4}\left((-1+2n)3^n+1\right)$
$=\dfrac{3}{4}\left((2n-1)3^n+1\right)$
ふ~、やっとできました!
$\dfrac{1}{4}\left((2n-1)3^{n+1}+3\right)$
でもいいし、無理にカッコでまとめない答えだってOKですよ。
でも $3^n$ と $3^{n+1}$ はひとまとめにした方がきれいですね。
これで大丈夫ですか?
こんにちは。 回答ありがとうございます。 一つ一つの手順を丁寧に書いてくださるのでとても分かりやすいです。 自身で解いていた時はごちゃごちゃしてしまい、頭がこんがらがってしまっていたので大変助かりました。 ありがとうございます。
はい、どういたしまして。またどうぞ。