このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
数列の和
写真の問題(2)についてです。
解答と自身の解が合っているか確認して欲しいです。
解答は自身の解の
(−1)^n+1から一つ分(−1)を出して(-2n+-3)に掛けてマイナスを打ち消して整理した形と考えて良いのでしょうか?
【写真】
1枚目→問題
2枚目→解答
3枚目→自身のノート
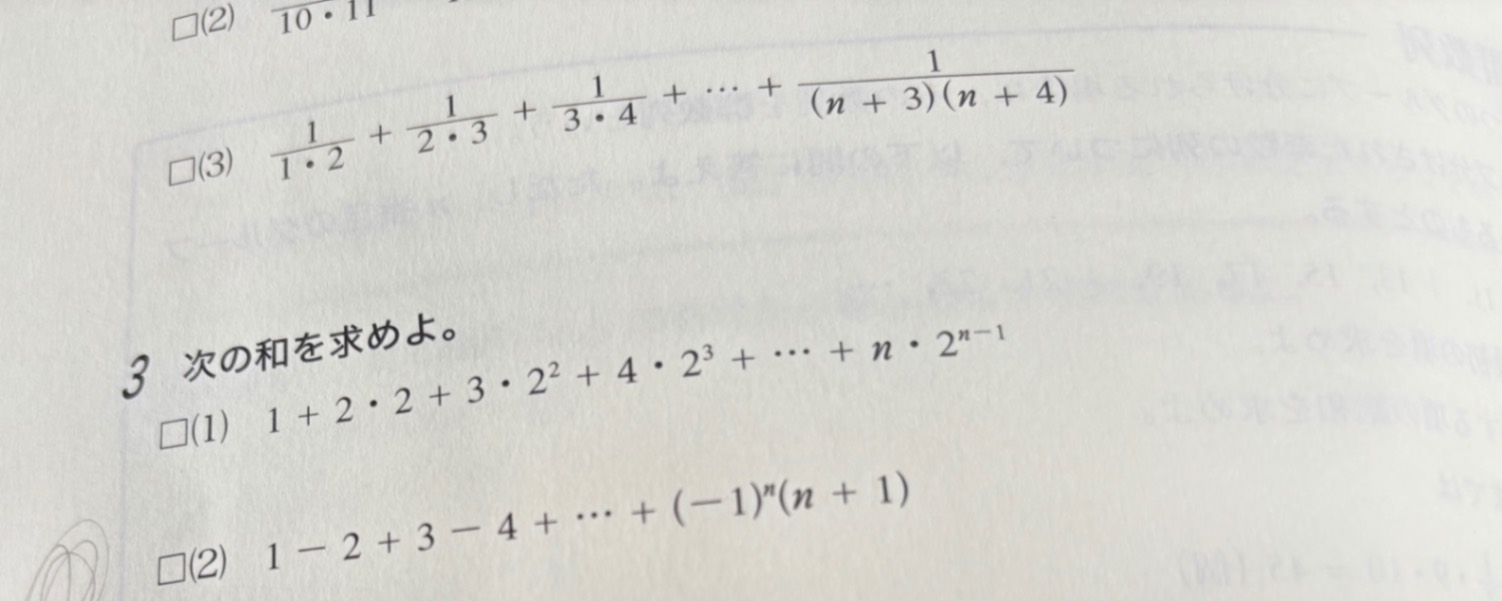
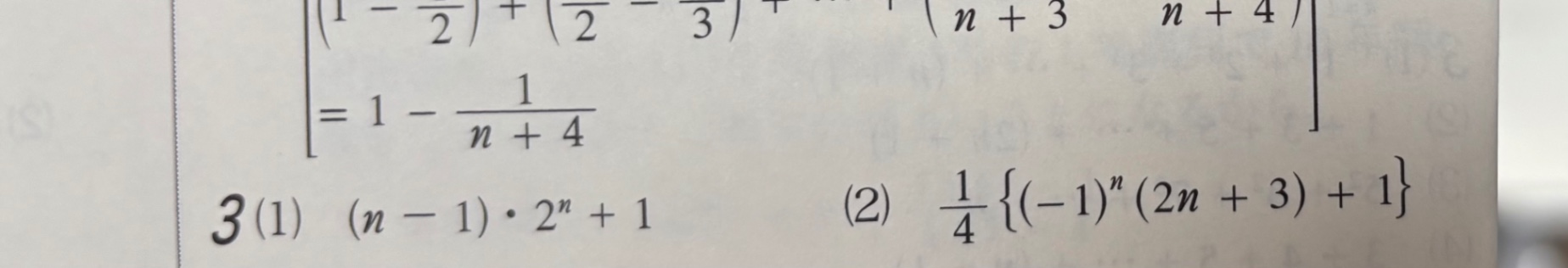

回答
ひなた さん、こんにちは。
あなたの答で間違いはありません。
「…マイナスを打ち消して…」という考えも大丈夫です。
さて、どちらが式としてきれいか、美しいか、と言えば、残念ながらマイナスを処理した方ですね。
あなたの式のままでもマルはつくでしょう。が、-1点くらいの原点はされるかもしれません。
(-1)の累乗があって、掛け算しているカッコの中がマイナスなら、そのような変形は考えるべきです。
たとえ累乗がn+1でなくnであってもマイナス一つ分をカッコの方に入れて$(-1)^n(-2n+7)\to (-1)^{n-1}(2n-7)$ あるいは $(-1)^n(-2n+7)\to (-1)^{n+1}(2n-7)$ とすべきでしょうね。
数学には「美しい」という考えがあるのです!美しいほうが良い式なのです。
1つの問題の解法だっていろいろありますが、より美しいものを良しとします。
これで大丈夫ですか?
回答ありがとうございます。 「数学的により美しい式」 の基準としては、マイナスをよりミニマムに表現できるかどうか。みたいな視点なのでしょうか?
そう一概には言えませんが。でもマイナスが少ないというのは美しいほうですね。
そうなんですね。 返信ありがとうございます。
どういたしまして。