このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
一次関数
この一次関数がわかりません
①はできました
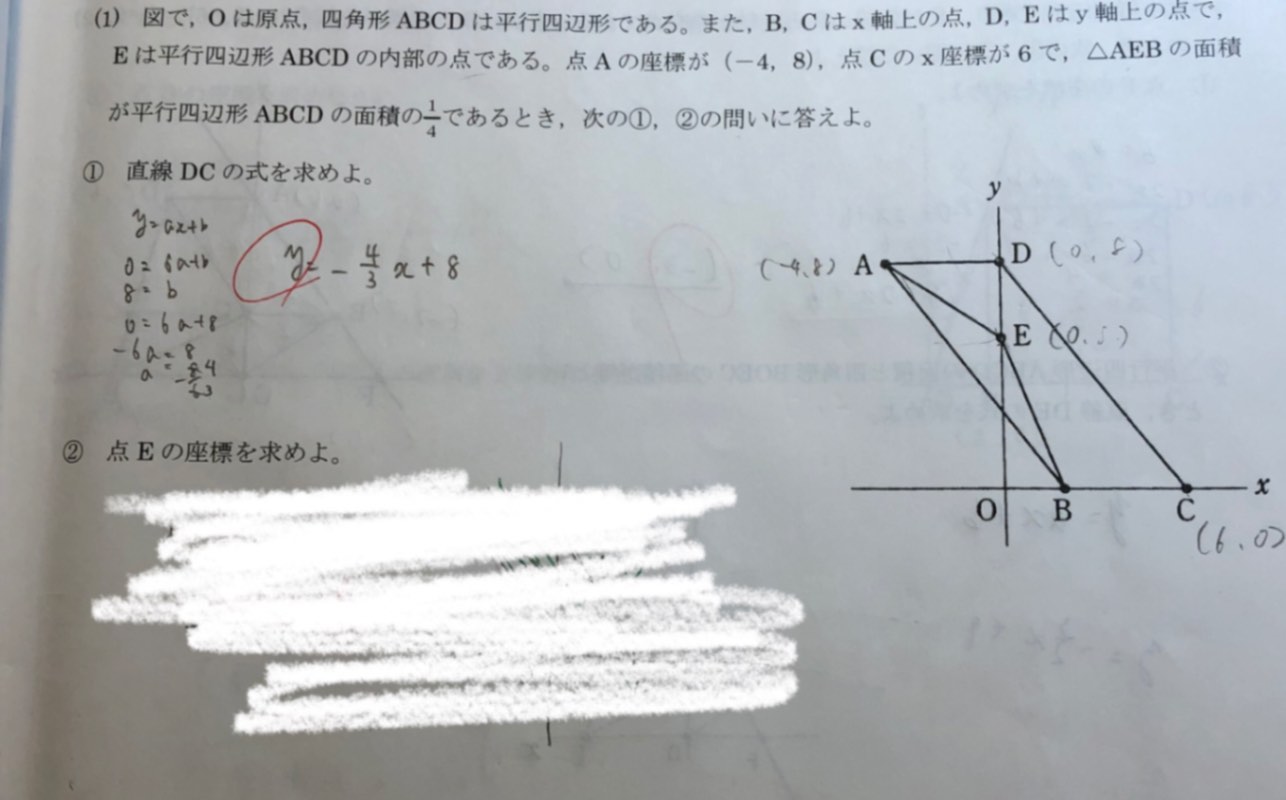

回答
長岡 真奈 さん、こんにちは。初めての方ですね。よろしく。
ここは質問箱なので…なるべく具体的な質問をしてほしいのです。あなたがどのような方針でやってみたのかというのは、これからのアドバイスに重要です。なんか、白で消されちゃってますが、次回からは自分のやったところまでは見せてくださいね。
それから、ここではなるべくあなたにも考えたり計算したりしてほしいので、まずはヒントや方針を書きます。
それですこし進めてみてください。行き詰まるようなら、言ってくれればその先のヒントなど書きますので。
(意地悪なのではありません!あなた自身がやらないと力にならないと思うからです)
また、1次関数の問題ですが、図形の性質なども使います。あなたは中学?高校?何年生ですか?
平行四辺形の性質は学習済み?等積変形ってわかりますか?
この問題は、いろいろなやり方があります。
等積変形もうまい手ですが、まずは図形として解く方法を書きますね。
まずBの座標を求めておきますよ。
ABとy軸の交点をFとしておきます。直線ABの式は分かりますね。そこからFのy座標が分かります。
また平行四辺形の面積も大丈夫ですね。その1/4を計算しておいてください。
Eのy座標をpとしておいて、△AEBの面積を2つの三角形△AEF+△EFBとして求めることにします。
どちらの三角形も底辺をEFと考えれば高さはEDとOBです。EFの長さはp-(Fのy座標)です。
これで△AEB=△AEF+△EFBがpを使って表わせますので、それが1/4の面積に等しいという方程式からpが求まります。
別のやり方は、平行四辺形の対角線の交点をQとしたら△QABの面積は平行四辺形の1/4です。あとは△QABの頂点QをABに平行に動かしてy軸と交わる点を見つければ、それがEです。これだと面積の計算は不要です。
どちらでも、できそうな方で進めてみてください。
ここでは会話型を目指しています。できればあなたの途中までのノートを見せてもらいながら、何回でもやりとりして納得できるまで解説しますよ。
それでは、これを読んだら、わかったとか、できたとか、まだこのへんがわからないから説明してほしいとか、ここまでいったが行き詰まったとか、コメント欄になにか返事を書いてください。お待ちしています。
================================
追記 2025/08/15 17:25~
コメント拝見しました。
塾の問題ですか!それならマンツーマンで塾の先生に聞くのが一番いいと思うのですが、無理なのですか?
平行四辺形の面積の1/4は「÷4分の1」ではなく÷4か×1/4ですね。4×8÷4=8です。
上に書いたことに従ってやっていきましょうね。
確認ですが、Bは(2,0)と分かりましたか?これは関数で考えるより、平行四辺形の対辺の長さは等しいからBC=4.ここから6-4=2で出ます。
あ、Fの座標を求めなければ。
直線ABの式を求めて、その切片がFのy座標ですね。
①2点A(-4,8)B(2,0)をとおる直線の式は求められますか?
②$(0,\dfrac{8}{3})$ になるのですが。
Eの座標を(0、p)としておきます。pをこれから求めようとしていますよ。
③△AEF=1/2×EF×AD=1/2×(p-8/3)×4=…
④△EFB=1/2×EF×OB=1/2×(p-8/3)×2=…
⑤よって△EAB=△AEF+△EFB=(整理して)=…
⑥これが8なのですから=8と書いてpについての1次方程式になります
⑦これを解けばpが求まり、Eの座標は(0、□)と求まりますよ。
〇の番号の何番までできますか?
これで自力で求められましたか?
コメント欄になにか返事を書いてください。がんばりましょう!
塾の先生はどんなやり方で教えてくれたのでしょうか?
これと同じ?
=============================
追記 20:35~
追加された写真は何でしょうか?
塾での説明かな?
それを見て、もっと簡単な解法を思いつきました、というか気が付いていませんでした。
ひょっとすると塾では…
「BCの中点M(4,0)を通ってDCに平行な直線を引いたときのy軸との交点を求めればいい」なのかな?
確かに、これだと(1)を利用していて、いかにも(2)らしいですね(笑)。
△AMBの面積は平行四辺形の面積の1/4です。
頂点MをAB(あるいはDC)に平行に動かしても面積は変わらない(等積変形)から、「BCの中点M(4,0)を通ってDCに平行な直線を引いたときのy軸との交点を求めればいい」ということになりますね。これの方が楽ですね。
ごめんなさい 平行四辺形の4分の1は 4✖️8➗四分の一ですか? 理解力が全くないのでここまでしかできませんでした。 中学生です 等積変形も学習済です。 白のところは塾で受けた解説と先生のお名前が書かれているのでお見せできません 本当にごめんなさい。
上の回答に追記しました。読んでください。
3枚目が塾での解説を写したものです 自分でも何書いてるのかわからないです 2枚目のところまでできました その後がわからないです
移項して➖3P🟰➖8 P🟰8 ってことですか!?
P🟰3分の8
はい、p=8/3(3分の8)ですね。それでいいです!もう大丈夫ですか?
はい、ありがとうございました!
新しい写真を見ました。上の回答に追記しましたので読んでください。
ありがとうございます
どういたしまして。せっかく塾に通っているのなら、直接人間(先生)に質問した方があなたに適する説明をしてくれるように思えますが。ま、もちろんこのサイトで聞いてくれてもいいのですが、このようなテキスト文での説明には限界があります。