このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
三角関数
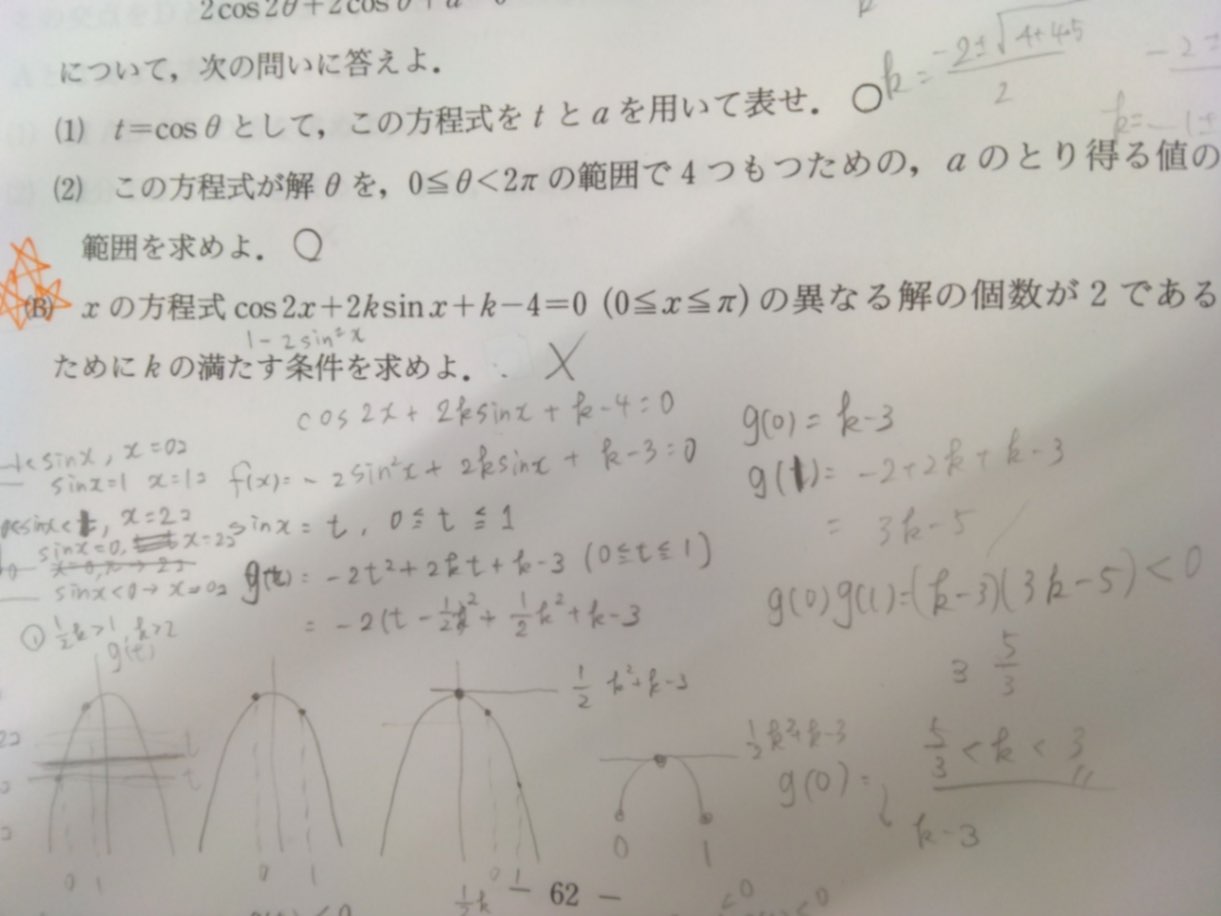
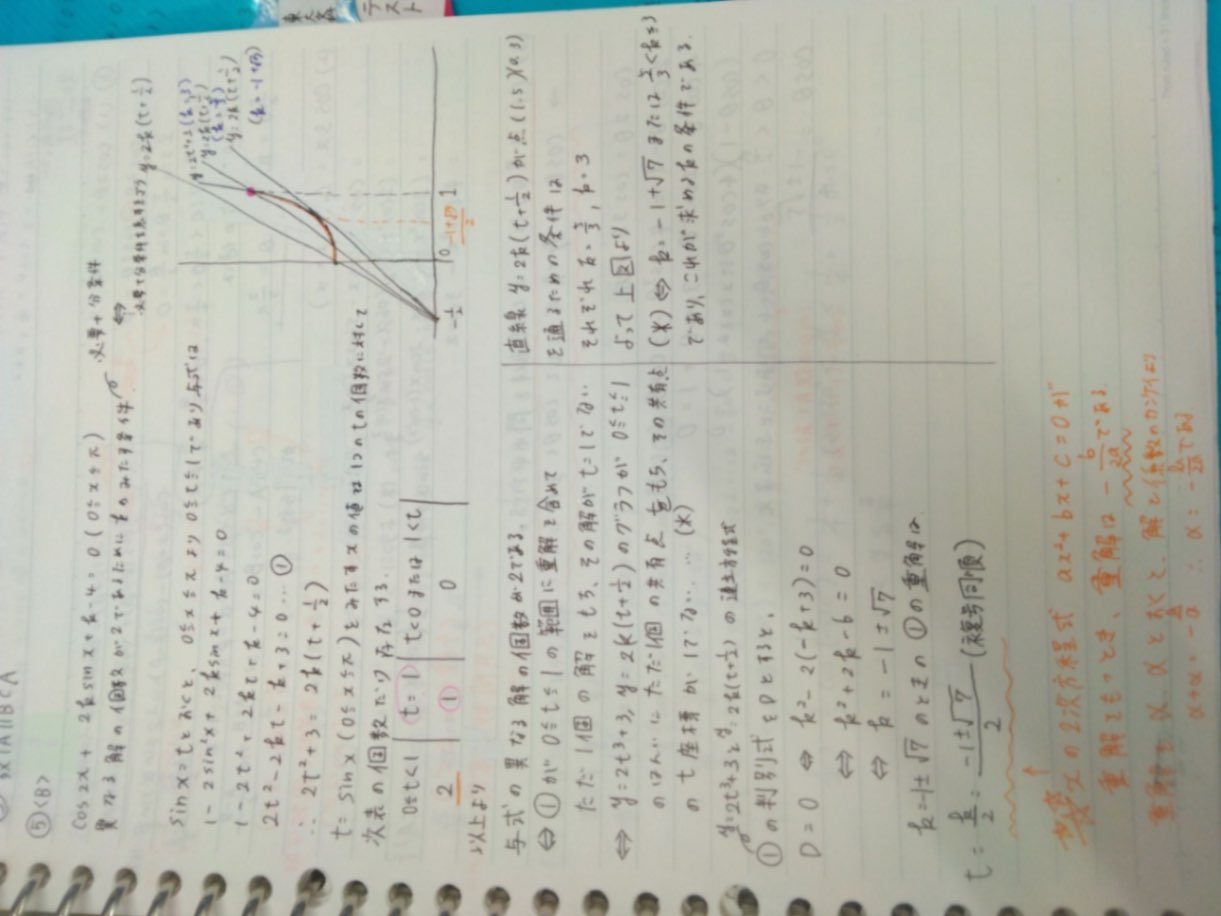

回答
あなたの答案の(イ)ですが、接する場合だけではなく、y=0がf(0)とf(1)の間にあってもいいのではないですか? ▶︎y = f(t)とy = 0の交点が範囲内に2個あるということでしょうか…?交点2個だとすると0 < t < 1の範囲なので解xは4つになりませんか? また、(ア)で3に等号が入るのは、t=0が解の場合もx=0、πの2解が得られるので、条件としてはf(0)≦0なのです。 ▶︎よくわかりました!!ありがとうございます!! 軸の位置は気にせずに場合分けは3つ。 ▶︎二次関数の解の配置問題って ・端点 ・判別式 ・軸の位置 の三条件がいると思ったのですが、今回軸の条件がいらないのはどうしてですか?
▶1:「y = f(t)とy = 0の交点が範囲内に2個あるということでしょうか…?」あ、いや、そうではないです。あくまでもf(0)とf(1)が異符号だと言っています。範囲内のグラフの端点がⅹ軸の両側になるということです。その表現で「交点は1つ」になりますよ。軸が0から1の範囲外ならばもちろん交点は1個だし、軸がその範囲内でも直線y=0は2回は交われないです。必要なら図も書きますが、あなたも図を書いて確かめてみてください。 ▶3:たいていの場合はその3つ、あるいはもっと必要になるような配置問題もありますが、必ずしもいつでも必要というわけではありません。一番単純な例では「2次方程式x²+ax+b=0が正と負の解を一つずつ持つための条件を求めよ」では「f(0)<0」だけで十分だし、「2次方程式x²+ax+b=0が2つの実数解を持ち、1つだけが0と1の間に解を一つだけ持つような条件を求めよ」では「f(0)f(1)<0」だけでいいです。しつこいですが(笑)「2次方程式x²+ax+b=0が1と2の間と3と4の間に一つずつ解を持つような条件を求めよ」も軸なしでいけますよ。 これでどうでしょうか?
図も含めて自分で考えてみます!!ありがとうございます!!
どういたしまして。行き詰まったら言ってください。