何の計算式、公式が適応出来るかの相談です

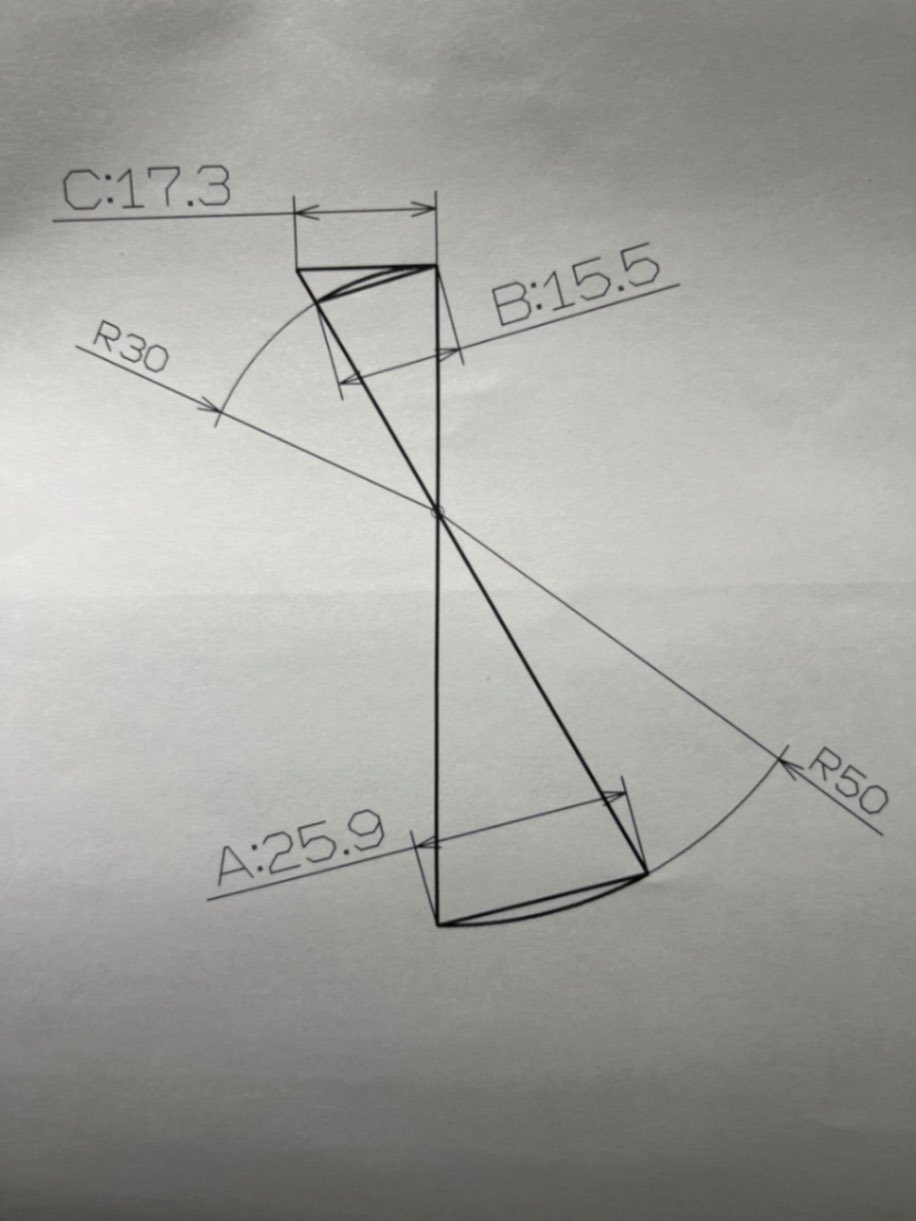
添付画像のAからBは比率で算出できますが、AからCを求める場合の計算式が分かりません。 三角関数かとも思ったのですが、画像の場合は直角三角形ですが、そうではない場合も当然あり、アドバイスが頂きたいです

スリム　ゴリラ　さん、こんにちは。はじめての方ですね。よろしく。 さて、図の一番上にある線分の左端が定まる情報がありません。 そうなると、このままではCは求まりません。 何か情報が抜けている？ 会話形を目指しています。コメント欄に何か返事を書いてください。よろしく。 ================================ 追記　2025/08/21　14:45～ 接しているという情報が分かれば、三角比を用いて出せることは出せます。 余弦定理などは大丈夫でしょうか？ ３０と１５．５を使います。 上部の三角形だけで出ます。点に名前がないのでつけますね。 上の線分の左端をA,右端をB、砂時計のくびれたところをCとします。 AC上にある交点をDとします。CD=CB=３０ですね。また∠ABC=９０°です。 △CBDは2等辺三角形です。 この3辺の長さはわかっているので、余弦定理からcos∠DCBが求まりますね。 cos∠DCBからtan∠DCBを求めます。 そうすればAB=CB×tan∠DCBで求まりました！ 実際の計算は電卓とかでやらざるを得ないようですね。 これで大丈夫ですか？ ここでは会話型を目指しています。これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。お待ちしています。