このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
数2 図形と方程式
写真は順番に問題、解説、自分の考えた解き方です。
線分Lと放物線が共有点を2つ持つ場合についてです。
最後の写真は四角で囲っているところが出た必要条件で、一番最後の四角で囲ったところが違いました。
解答解説も納得できるのですが、自分のやり方もなぜ間違っているのかわかりません。もしわかったら、教えてください!

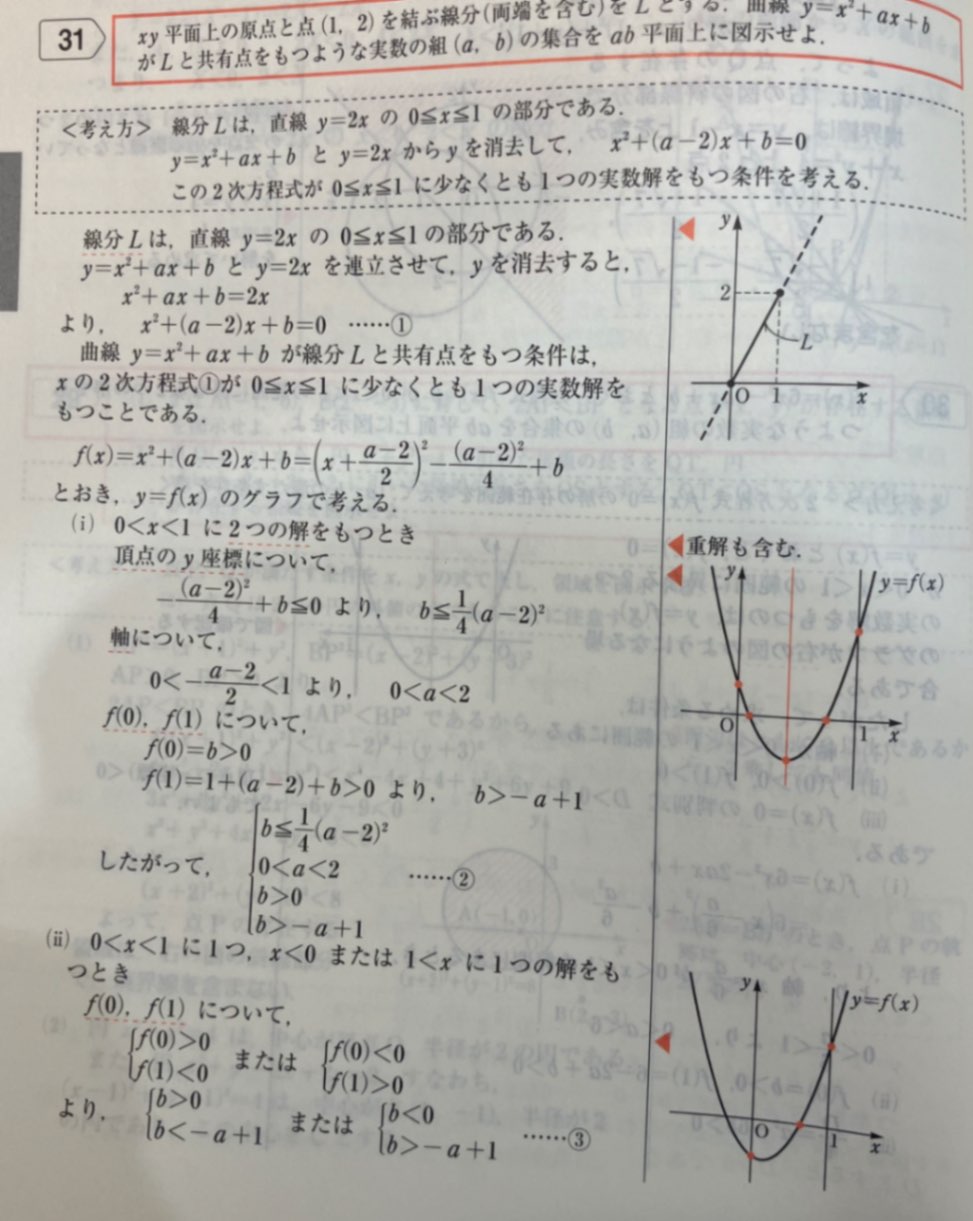
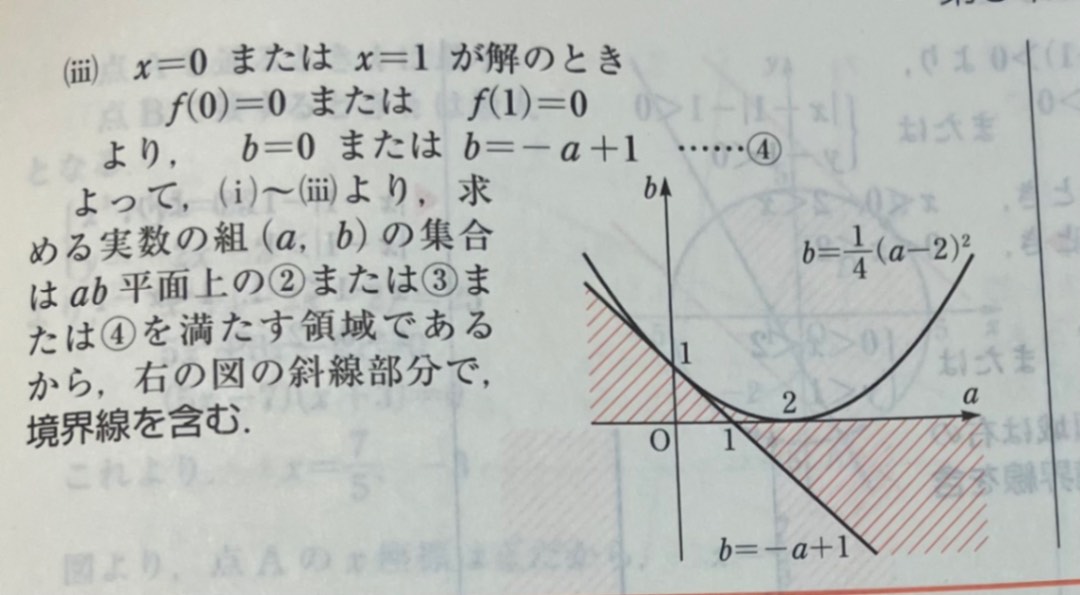

回答
Yuko さん、こんにちは。久しぶりですね。
さて、あなたの答案を拝見しましたが、ちょっとあなたの意図が読めません。
出来ればもう少し言葉を添えた答案を書くべきです。
まず、f(x,y)という2変数関数は何を意味していますか?というより、そのyは何でしょうか?
ひょっとして2xのこと?もしそうなら、f(x,y)は不要で、y(2x)≦x²+ax+bで十分ですね。
後半、放物線の軸が0と1の間だとしていますが、それは必要条件ではありません。
軸が0と1の間になくても放物線と線分は2点で交わることができますよ。際どいですが図を書いて試してみてください。
いずれにしても、あなたの答案は(特に後半)放物線だけ考えていて線分についての考えがなくなってしまいます。
交点はあくまでも2つの図形の位置関係ですから、後半のような考えではなかなか厳しいと思います。
交点は連立方程式の解、ということを徹底していないと。
連立させてxの2次方程式にして、それについて考えないとうまくいかないと思います。
こちらの理解不足かもしれませんが、できればもっと言葉を添えた答案を書くように心がけてください。
これで大丈夫ですか?コメント欄になにか返事を書いてください。よろしく。
f(x,y)=x^2+ax+b-yで、yを移動させてf(x,y)が正か負かによって線分が放物線の内側にあるのか外側にあるのか判断しやすくすると良いのではないかと考えました。 また、この軸が0と1の間になくても2点で交わる場合がわからないので、教えてください!
①f(x,y) については、あなたが使いやすいのなら構いませんが、答案としては、なにか説明が欲しいところですね。 ②放物線の2乗の係数が1なので、頂点から右に1、上に1だけ進んだ点も放物線上にありますね。そこでの接線の傾きは2です。その接線をちょっとだけ左に動かすと、軸の右側で2点で交わることになります。その2交点を含むxの範囲が0と1の間にあるような状態は考えられますね。このような状態があるので軸が0と1の間にある必要があるというのは間違いなんです。 これで大丈夫ですか?
なるほど、理解できました。あと説明ももう少し丁寧に書くようにします。ありがとうございます。
お役に立ったのならよかったです。またどうぞ。