このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
放物線と円の共有点・接点
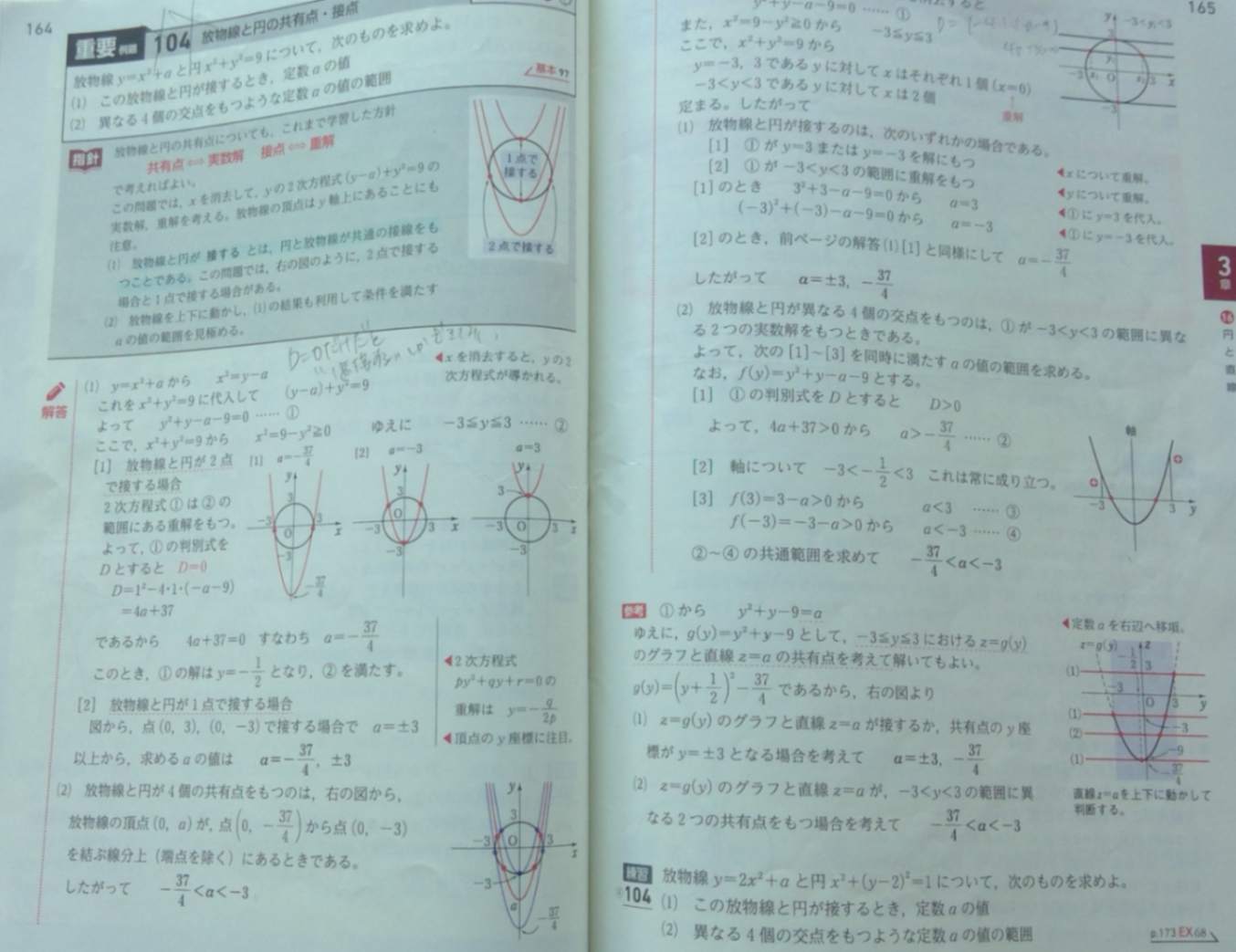
回答
教えてくださりありがとうございます。 判別式が使えるという前提で、 D=0は図形が1点で接していても2点で接していても使えるということですか?
いや、D=0は重解になるときで、この場合はyについて重解になります。それに従ってxが2つ出てきて「接点が2つ」という状態であることが分かります。どの文字の2次方程式なのかは意識した方がいいですね。
すみません、体調を崩していました(います)。返答が遅くなっていて申し訳ないです。 今回の場合だと一つのyに対してxが二つのため重解ですが 直線と放物線が接するときD=0を使いますがそれも重解なのでしょうか?一つのx(y)に対して2つのy(x)があるわけではないですが...。放物線と直線の式をまとめたxの2次方程式に関して、xの解が1つしかないから重解ということですか?
あれあれ、暑い中大変ですね。お大事に。 「一つのyに対してxが二つのため重解です」という考えはちょっと違うような。 その場合では、yについての2次方程式の解は本来2つあるのですが、それが重なって1つに重なったときだから重解なんですよ。xが…というのは関係ないです。 直線と放物線の場合も、本来なら荒天が2つあったのに、その2つが重なってしまったときが重解です。ま、たしかにxの解が1つしかないからではあるのですが、重なった解すなわち重解という理解が必要です。 これで大丈夫ですか?
わたしにとって少し難しいです....。問題文の中でD=0を使っていいか考えるときは、接線が共通するかどうかで考えればいいのでしょうか?
重解と判別式は区別しましょう。交点の座標を求めようとする方程式が2次方程式の場合は(対象が2次関数でも2次曲線でも直線が相手でも)判別式=0でいけますよ。3次方程式の重解とか、4次関数のグラフと接するような問題では判別式は使えませんし。これからも重解や判別式を使わなければならない問題とはたくさん出会うはずなので、やりながら理解を進めましょう。たくさんやるとコツも分かってきますよ。
お返事ありがとうございます。 交点の座標を求めようとする方程式が2次方程式の場合は(対象が2次関数でも2次曲線でも直線が相手でも)判別式=0でいけるというので納得できました!たくさん練習します...!
そうです! 体調大丈夫ですか? がんばってください!
少しずつ治ってきています💦もっと頑張ります...!