このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
数学的帰納法
写真の問題(2)についてです。
3枚目の写真の部分からどのように進めれば良いのかわからなくなってしまったので教えていただきたいです。
【写真】
1枚目→問題
2.3枚目→自身のノート
(追記: 2025年8月28日16:55)
4枚目→追加ノート写真
返信するのが遅くなり申し訳ありません🙇
お陰様で解けました。
Goleに無理やり持っていくための発想が自ずから湧いてくる気が全くしないのですが、やはり問題を解いた経験からそう言ったスキルは身についていくのかと思いますので、今後もバシバシ教えてくださると嬉しいです。
今回もご丁寧にありがとうございました。


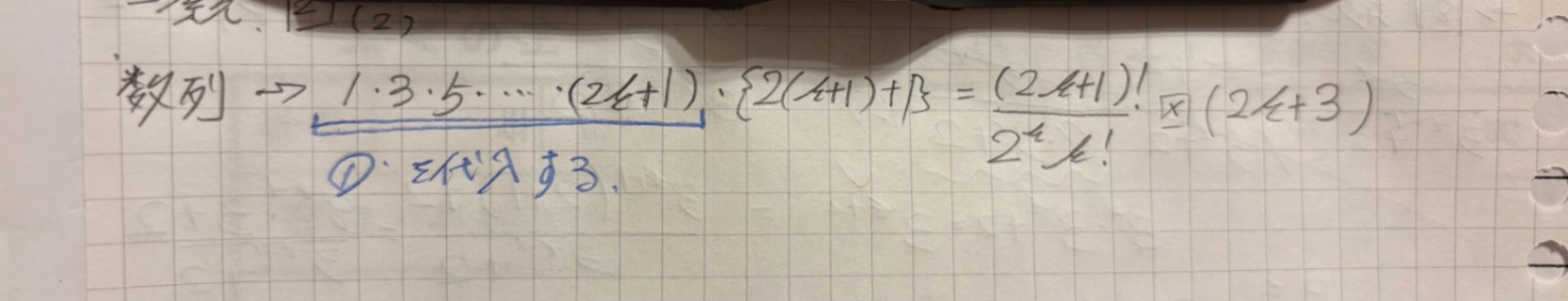

回答
ひなた さん、こんにちは。毎日暑い日が続きますね。
最後の式も目指すGoalもそれでいいのです。数学的帰納法の後半は「無理やりゴールにもっていく」です。
最後の行の式とゴールとを見比べて、一番わかりやすい違いは分子の階乗のところです。
(あれ?nなの?hなのkなの?kでいきますよ。)
(アルファベットがはっきりしない!採点者が読み間違う心配がありますよ)ズバズバ!
ゴールは $(2k+3)!$ なのに、最後の式は $(2k+1)!\times (2k+3)$ なので、分子に$(2k+2)$ を追加すれば分子の階乗の部分は同じになります。分子だけに追加するわけにはいかないから分母にも…
というのがヒントです。この先はやってみてください。
(意地悪じゃないです!自分でやらないと感動しないし、力がつきませんので。)
うまくいかないときはコメント欄で聞いてください。
これで大丈夫ですか?
=======================
追記 2025/08/27 9:00~
コメント見ました。
では…
最後の行の式の分子は1から2k+1までの自然数の積に2k+3がかかっています。
2k+1と2k+3は1つ飛んだ自然数で、間に2k+2があればつながって
1から2k+3までの自然数の積 (2k+3)! つまり (2(k+1)+1)! となり、ゴールの分子が作れますね。
分子に2k+2を勝手にかけたので、分母にも2k+2をかけざるを得ません。
最後の1行の分母は $2^k k!\times (2k+2)$ になり、2k+2を2(k+1) としてやれば
分母は $2^k k!\times (2k+2)=2^k k! \cdot 2\cdot (k+1)=2^{k+1}(k+1)!$ となってめでたしめでたしになるのです!
これで大丈夫ですか?
回答ありがとうございます。 文字の入った階乗の値にどのように計算すれば良いのかが分からないのです。 また 「(2k+2)を追加すれば階乗が同じになる」 というのも何故そうなるのかが分かりませんでした。 分からない事ばかりで申し訳ありませんがもう少し細かく教えてくだされば嬉しくです。
了解です。上の回答に追記しましたので読んでください。
追加の方に返信させて頂きました。 ありがとうございます。
答案、見ました。それで筋道はOKです。分母の話のところでkではなくk!です。!が抜けっちゃってます!!気をつけて!
本当ですね… ご指摘ありがとうございます‼︎