このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
直線周りの回転体の体積
y=xを座標軸と置いて進めています。
hは断面積の変数、tは積分変数と置きました。
tをどう表せばいいか止まってしまいました(;;)
また、X軸や原点周りに回転する解法、変数をベクトルで表したり方法もあるそうなんですが、どのように解くのが解きやすいですか?
↑直線が原点中心ではなく、角度も分からなかったりして時など少し捻った問題が出た時にも簡潔な解答になりやすい方法です(>人<;)

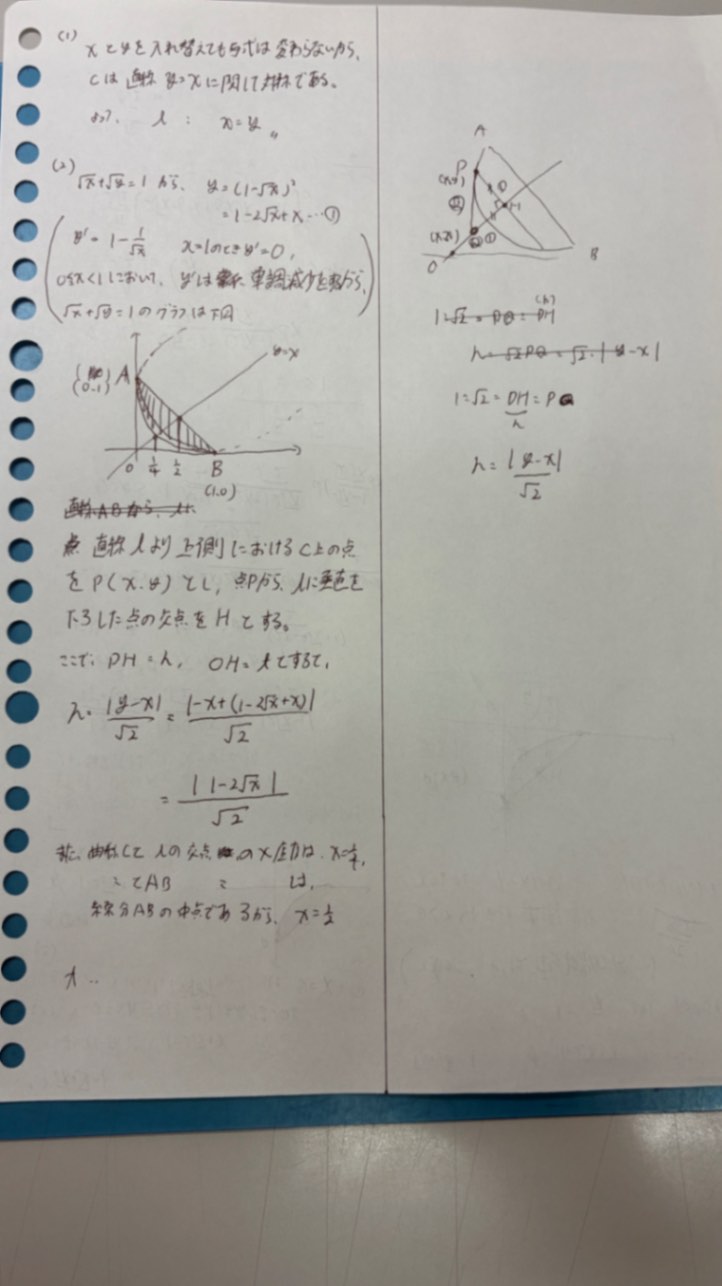
回答
い あ さん、こんにちは。
hについてはそれでいいです。hを考える時に△PQH(Pの真下がQだと見えるので)が45°45°の直角2等辺三角形を利用していれば、tについても気が付いて楽だったのです。PQ=y-xで、h=PQ/√2ですから。
tについても45°を利用して、t=OH=OQ+QH=√2x+hで求まりますよ。
あとはπh²をtについて√2/4から√2/2まで積分すれば求まります。
tはxで表わせていますので置換積分でdt/dx・dxとか積分範囲が1/4から1/2までとか変えて、積分計算をしてください。
やってみてうまくいかないようなら、途中までのノートをアップして見せてください。間違いを見つけたり、その先の方針など書きますよ。
これを読んだら、わかったとか、ここが分からないから説明してくれとか、コメント欄になにか返事を書いてください。お待ちしています。
後半のご質問は、具体的な問題でないと答えにくいですね。
https://hiraocafe.com/note/shajikukihon.html のページや、その冒頭にあるⅡやⅢへのリンク先を参考にしてください。
「斜軸回転体」で検索すればいろいろ出てきますよ。
うまくいきました(* • ω • )b △OHPで三平方の定理を使ってやってみても意外と綺麗にまとまりました!
あ、それならよかったです!またどうぞ。