このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
極限値
極限値を求める問題ですが
微分係数の定義に関する問題で(2)は(1)の誘導?で成り立っているみたいなんですけどよくわかりませんでした。解説をよろしくお願いします🙇
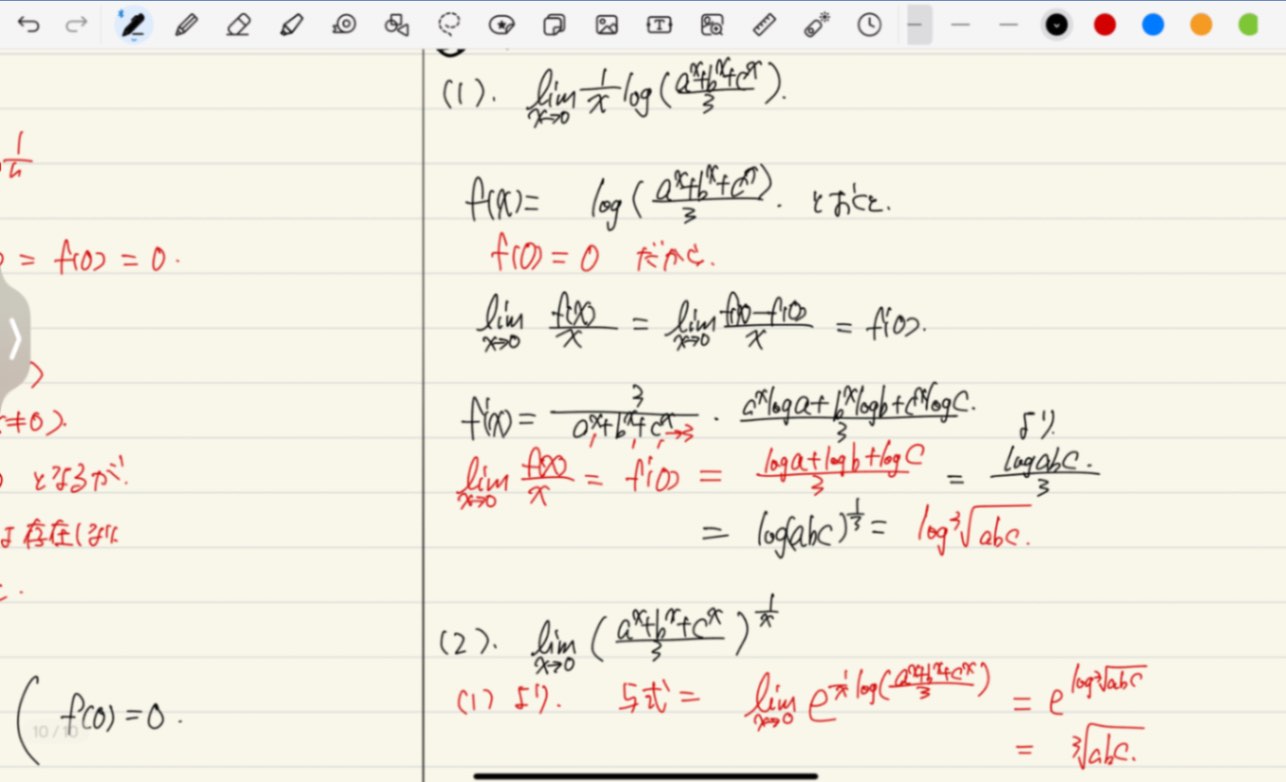
回答
間島 悠翔 さん、こんばんは。
(2)は微分係数の定義とは関係ないですね。
まず、次の等式は納得できますか?
$a=e^{\log a}$
対数の定義そのものと言ってもいいのですが、証明しろと言われれば
$p=e^{\log a}$ と置いて、両辺の対数を取れば
$\log p=\log a$
よって $p=a$
すなわち $e^{\log a}=a$ です!
今の問題では、上のaにあたるものが
$\left(\dfrac{a^x+b^x+c^x}{3}\right)^{\dfrac{1}{x}}$ ですので、
$\left(\dfrac{a^x+b^x+c^x}{3}\right)^{\dfrac{1}{x}}=e^{\log \left(\dfrac{a^x+b^x+c^x}{3}\right)^{\frac{1}{x}}}$
$=e^{\frac{1}{x}\log \left(\dfrac{a^x+b^x+c^x}{3}\right)}$
$\left(\dfrac{a^x+b^x+c^x}{3}\right)^{\dfrac{1}{x}}$ の極限を$e^{\frac{1}{x}\log \left(\dfrac{a^x+b^x+c^x}{3}\right)}$ の極限と考えて、全体の極限を指数部分の極限を先に考えてもよかろうと、(1)を指数部分に使ったということです。
その結果、$e^{log \sqrt[3]{abc}}$ が得られ、また $e^{\log a}=a$ を使って $=\sqrt[3]{abc}$ となったのですね。
これで大丈夫ですか?コメント欄になにか返事を書いてください。よろしく。
納得できました🙇 対数の復習をしときます
それならよかったです!またどうぞ。