このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
式変形
どうして3乗が出て来るのかがわかりません
よろしくお願いします🙇
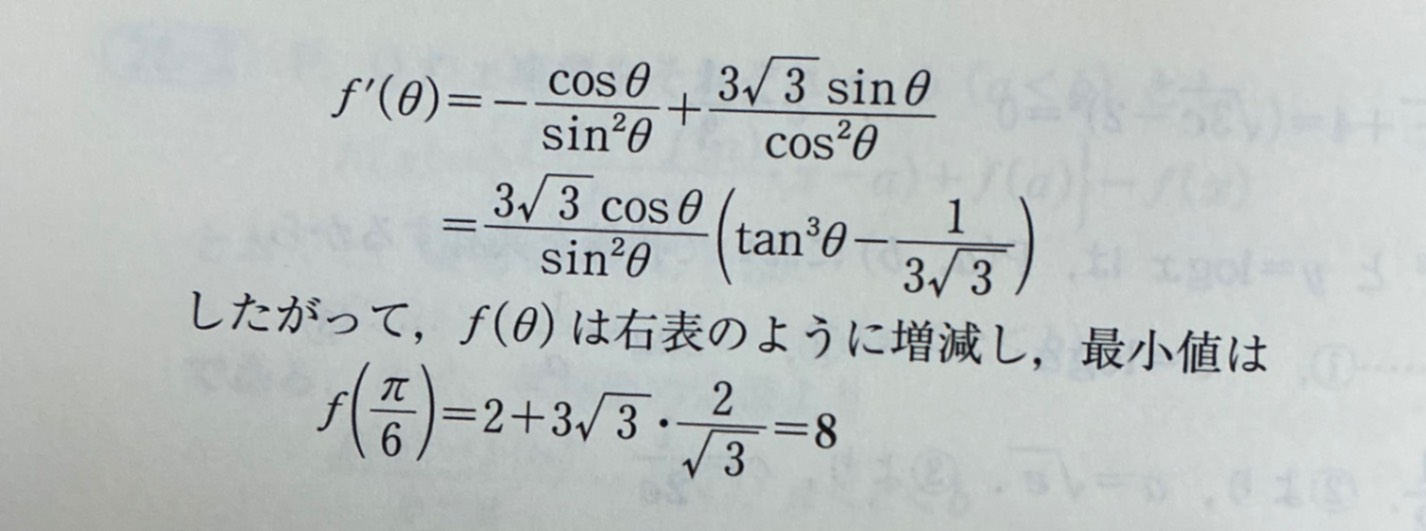
回答
間島 悠翔 さん、こんにちは。
う~む、かなり無理やりな変形なので、結果を見てなるほどと思うわけで、これをいっぺんに作るのは大変でしょうね。
とにかく $\dfrac{3\sqrt{3}\cos\theta}{\sin^2\theta}$ をくくりだしちゃえばたしかにそうなります。
$-\dfrac{\cos\theta}{\sin^2\theta}=\dfrac{3\sqrt{3}\cos\theta}{\sin^2\theta}\times\left( -\dfrac{1}{3\sqrt{3}}\right)$ だし、
$\dfrac{3\sqrt{3}\sin\theta}{\cos^2\theta}=\dfrac{3\sqrt{3}\cos\theta}{\sin^2\theta}\times \dfrac{\sin^3\theta}{\cos^3\theta}=\dfrac{3\sqrt{3}\cos\theta}{\sin^2\theta}\times \tan^3\theta$
だからね。確かにそこに書いてあるようにタンジェントの3乗ができますね。
しかし…どこからそんなものをくくりだそうという発想が生まれるのでしょうかね????
普通ならまず通分でしょうね。
与式=$\dfrac{-\cos^3\theta +3\sqrt{3}\sin^3\theta}{\sin^2\theta \cos^2\theta}$
これを見たら分子をコサインの3乗で割ってみようかという発想が生まれるのはそう難しいこと(突拍子もないこと)ではありませんね。
それで分母分子をコサインの3乗で割って整理すれば
$=\dfrac{\cos\theta(-1+3\sqrt{3}\tan^3\theta)}{\sin^2\theta}$
となって、f'(θ)=0を解くことができます。
これで大丈夫ですか?
理解できました!ありがとうございます
お役に立ったのならよかったです。またどうぞ。