確率

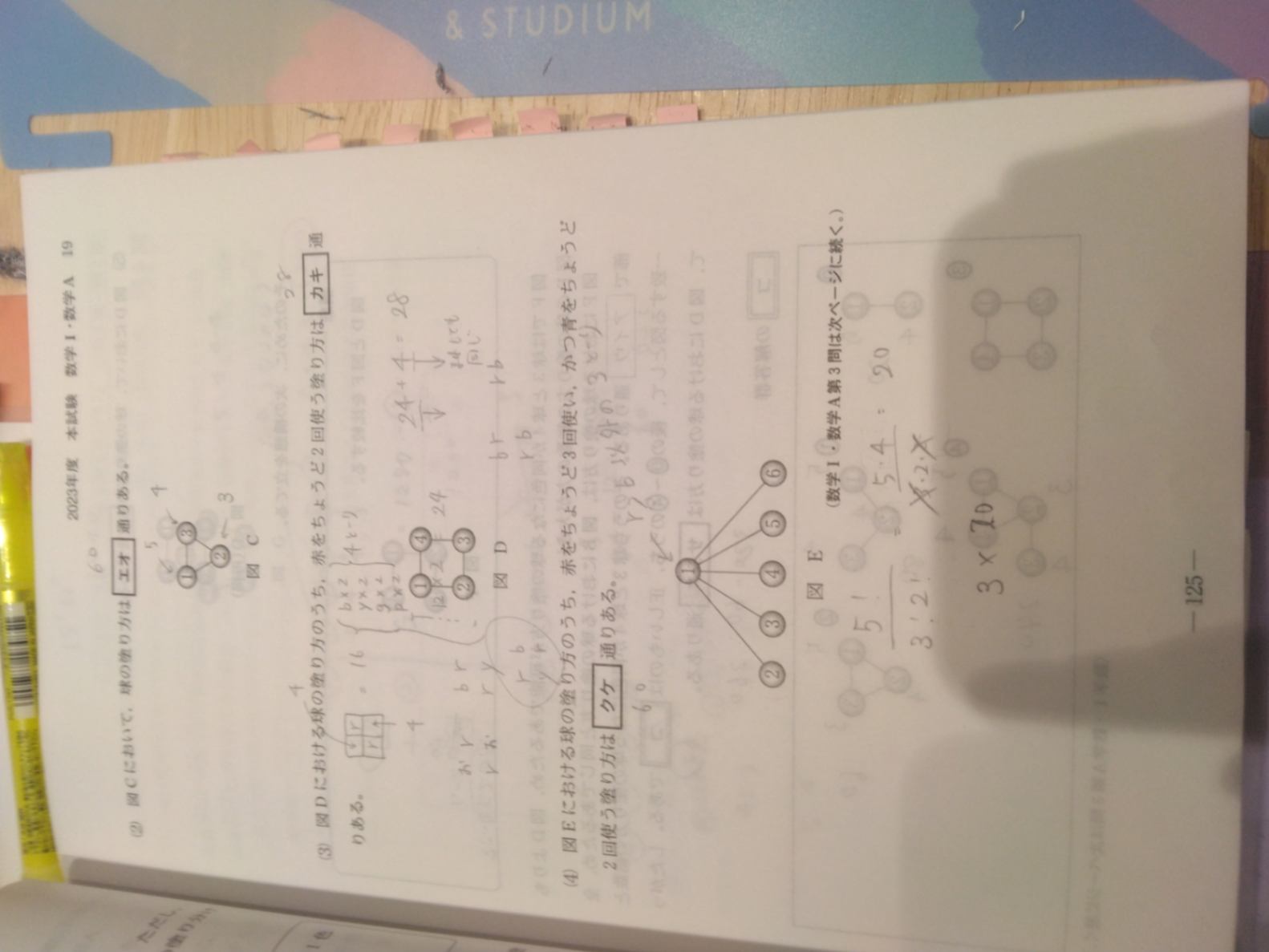
(3)(6)で質問です。 答えはそれぞれ(3)カキ32(6)セソタチ1020 です。 (3)は円順列の問題だと思い、赤と、ある1色で構成される場合は場合の数を2倍しませんでした。しかし、実際は2倍されるべきのようで答えは32でした。この問題がどうして円順列の解き方にならないのでしょうか？ (6)では①⑤が同じ色になる確率を(5)は使わず、メモのように5×4×4×3で解いたのですが、場合の数が20足りず誤りでした。私の解き方のどこがおかしいのでしょうか

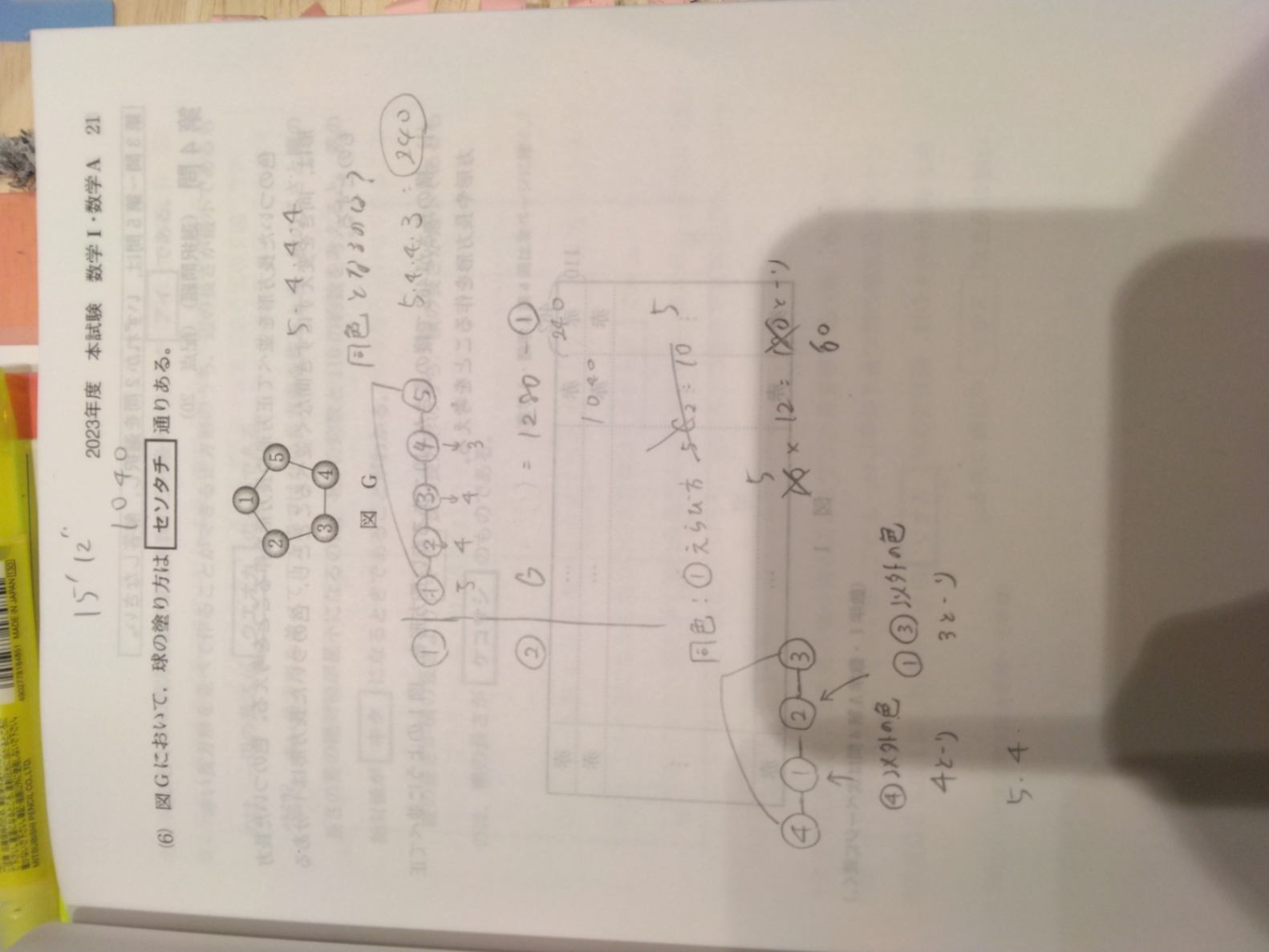
忠さん、こんにちは。回答が遅くなってスミマセン。 （３）は円順列ではありません。なぜかというと、球には番号が付いていますから、「回転しても同じ順列になる」ではないので。座席が区別できない（座席に番号が付いていないとか、全く同じ椅子だとか、方角は無視とか）ような席に円形に座る、みたいなのが円順列で、この問題では赤が１なのか２なのかは別ものです。 2か所の赤の選び方は2通り（１，３か２，４）。残りの2個が同色の場合はのこり4色だから4通り。残り2個が異なる色の時は「番号の若いほうが4色可能、番号が多いほうが残り3色が可能」で４×３＝１２。 よって２×（４＋１２）＝３２通り。 （６）は説明がないのであなたの意図が汲めたのかどうか心配ですが… 質問の際は、読めば意味がわかるくらいの答案を見せてくださいね。 メモだけではつかめないこともあるので。 １２８０を計算した式がないのでわからないのですが… また１２８０－２４０で１０４０なのかな？ 正解は１０４０より２０多いの？１０２０？１０６０？のどれなのですか？ あなたのそのような考え方では大変そうです（そうでもないか…）。①と④が(i)異なる色か(ii)同色かで場合を分ける必要がありますが、(ii)が実現できるには③が①と異なる色である必要があり、けっきょく場合分けが③が①と同色かどうかで分け、次に異なる場合は①と④が同じか異なるかで場合を分け…みたいにやっていきます。そのやり方で私は１０２０になったのですが、それは正解ではないのかな？それが正解なら説明も書けるのですが、間違っていたら意味ないし。 ちょっと正解を教えてください。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 追記　2025/09/01　16:00～ 正解の１０２０って質問の冒頭に書いてありましたね。見たのに読んでないという老人症状が出てしまいました。失礼！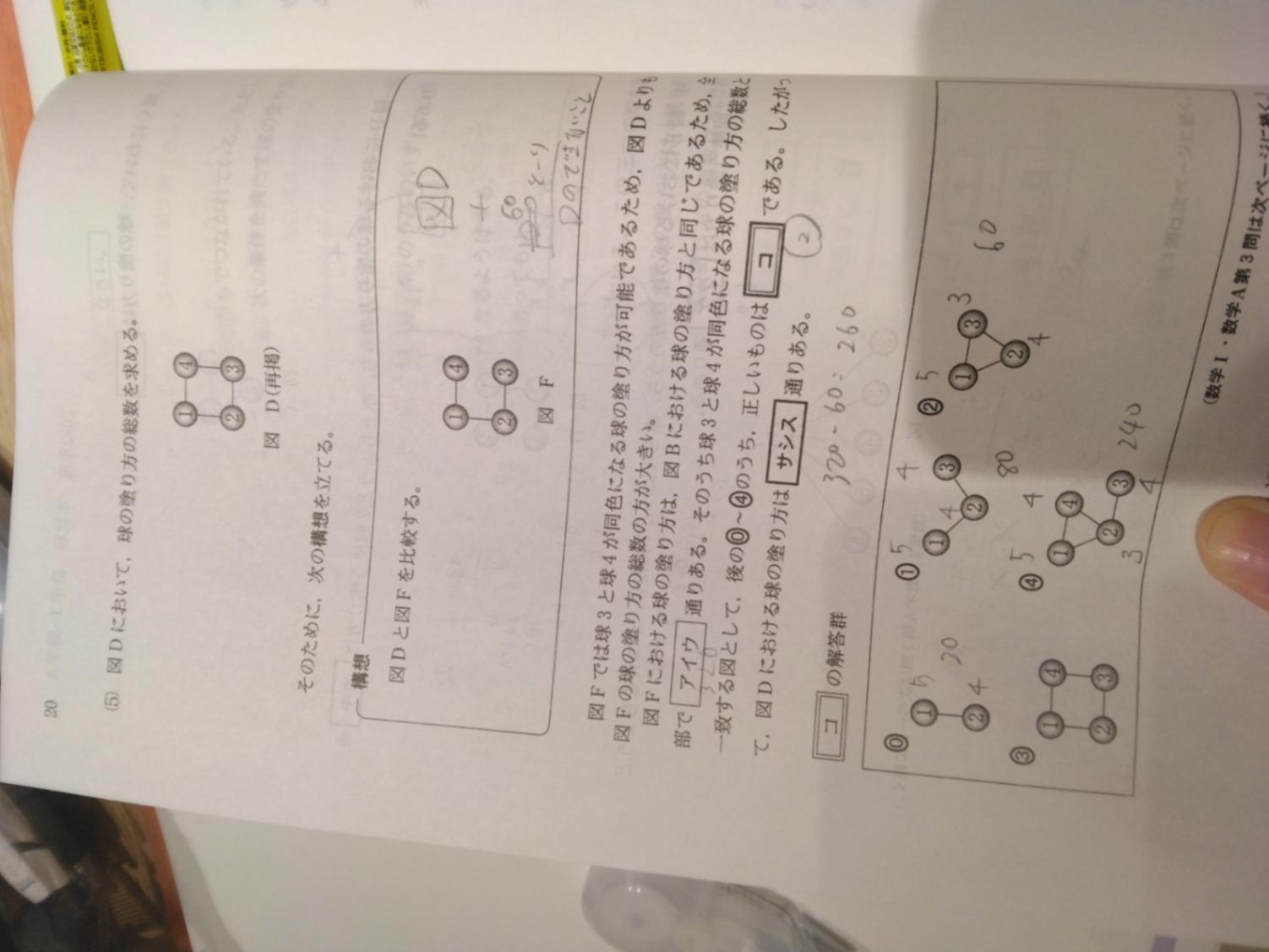 さて、正解が１０２０だとわかれば、（５）を使わずにやってみましょう。 ①から順に考えていくとき、上に書いたように③に何がくるかあたりから場合分けが必要になります。 ①は5通り、②は4通りまでは無条件で。さて③ですが、③が①と同色だと④が①と同色になることはなくなるので、ちょっと場合分けが始まります。 (ｱ)③が①と同色のときは、③までで５×４×１まで行きます。そのあと④は①③以外の4通り、⑤は①（＝③）と④以外の3通り。 よって5×4×1×４×３＝２４０とおり。 (ｲ)③が①とは異なる色の時は①②とは異なる3色で3通り。次に④が①と同色かどうかで場合が別れますよ。 　(ｲ-1)④が①と同色な時、5×4×３×1まできます。この時は⑤は①（＝④）と異なるから４通り。 　　よって5×4×３×1×４＝２４０通り。 　(ｲ-2)④が①と異なる色の時、④は①③以外の3通り。最後の⑤は①④以外の3通りが可能です。 　　よって5×4×３×３×３＝５４０通り。 以上をたして２４０＋２４０＋５４０＝１０２０通りとなります。 これでどうでしょうか？ あなたの5✖️4✖️4 ✖️4 ✖️4 ✖️4 は、①と同色になるかどうかの判断をしていないので、ちょっと無理ですね。