このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
三角関数 三角形の辺の長さ
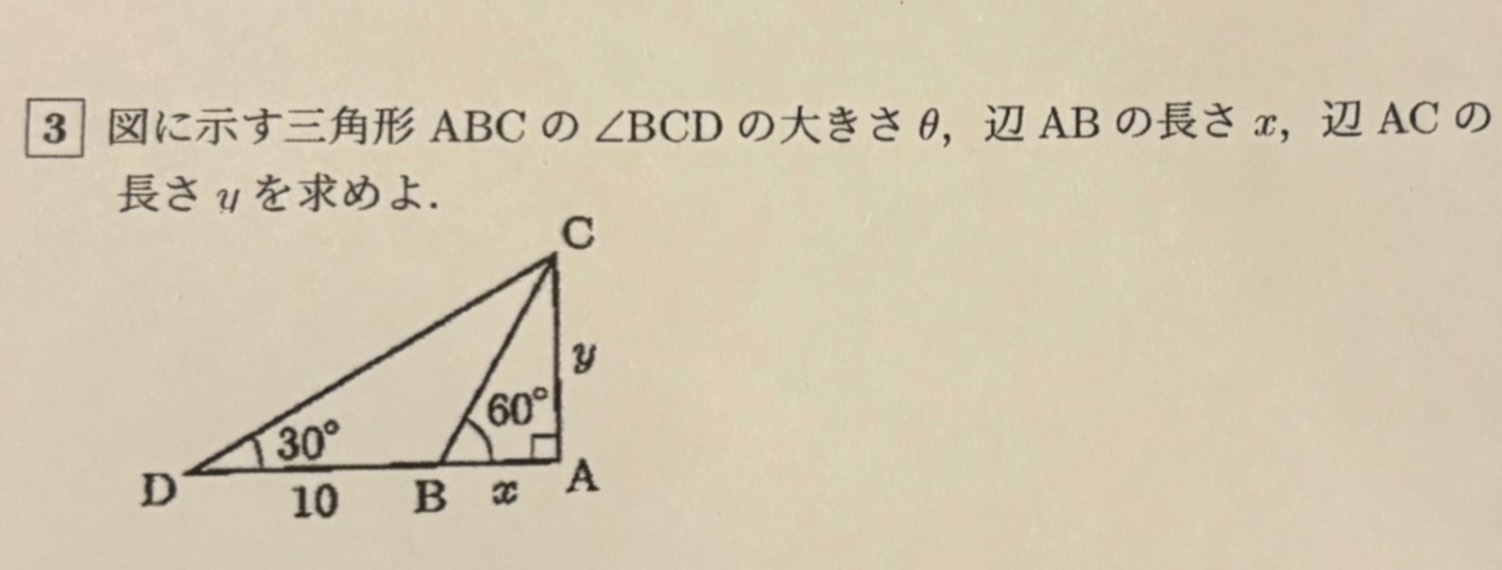
写真の問題を教えていただきたいです。
最初に相似で試したのですが解けず、AIに聞いたら単位円に当てはめるやり方(写真3枚目のような形だと思ってます)で解けると言われたのでやってみようと思いましたがわからなかったので質問させていただきました。
(どちらも消してしまいました)
ご回答よろしくお願いします。
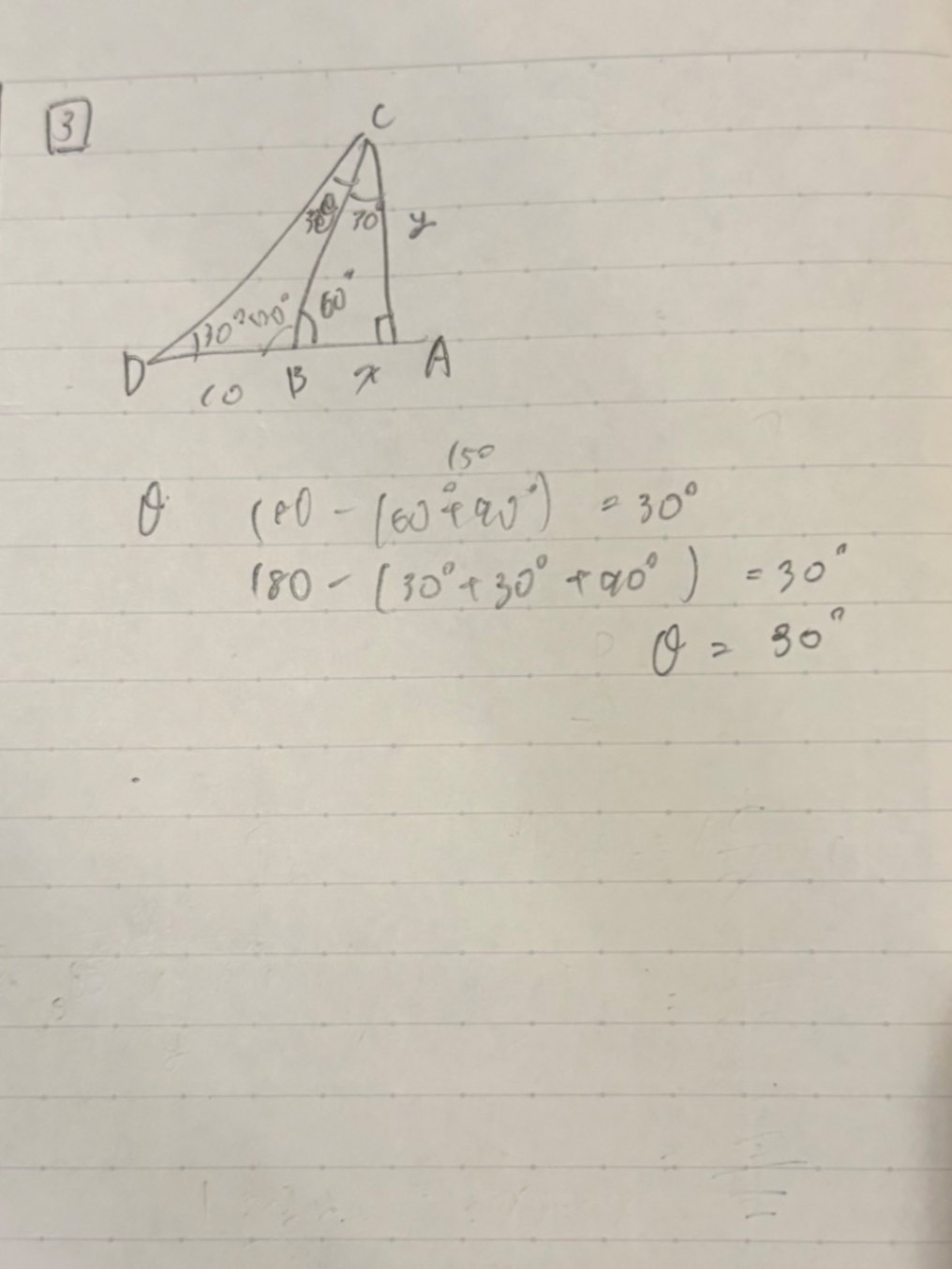
回答
くりさん さん、こんばんは。
ときどきAIに聞いたのだがわからない、という質問が来ます。私も試しに使ってみましたが、式の計算、因数分解とかごく簡単な方程式ぐらいは正確に解いてくれますが、文章で問題を与えるととんでもない答え(明らかに間違った答)を返してくることがあります。この問題も単位円は関係ないでしょうね。よほど高級な有料のAIならできるのかもしれませんが、無料で使えるオープンなAIはまだまだ未熟です。出された答が間違っていることを判断できればいいですが、そうでないと恥をかくことになります(笑)。人生相談や読書感想文くらいにして、数学はまだ使えないと思いますよ。まずは人間の頭脳を強化しましょう!!
∠BCD=30°が分かったのですから2等辺三角形が見えますね。
BD=BCですからBC=10。
次に△ABCは30°60°の直角三角形ですから、3辺の比は分かっています。大丈夫ですか?
1:2:√3というやつです。
BCが2の比率に対応する辺ですから、AB=xはBCの半分の5。ABが1の割合ですからAC=yは√3の割合。よってy=5√3です。
どうしても三角関数を使えというのなら、BCが分かった後に $\sin 60°=\dfrac{CA}{BC},\cos 60°=\dfrac{BA}{BC}$ と60°の三角比の値を使って求めてもいいですが。
これで大丈夫ですか?いつものようにコメント欄になにか返事を書いてください。よろしく。
くさぼうぼうさんこんにちは。 二等辺三角形までは見えていたのですが、その辺の長さが同じことに気がつけませんでした 無事解けました。 ありがとうございます。
それならよかったです。またどうぞ。