このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
三角関数
写真の問題(3)を教えていただきたいです。
ノートのように(1)と(2)と同じように解こうとしたのですが、$ \frac{1+tan5°}{1-tan5°} $となってしまいました。
これは答えにはならないと思うのですが、やり方が間違っているのかここからできることがあるのか教えていただきたいです。
ご回答よろしくお願いします。
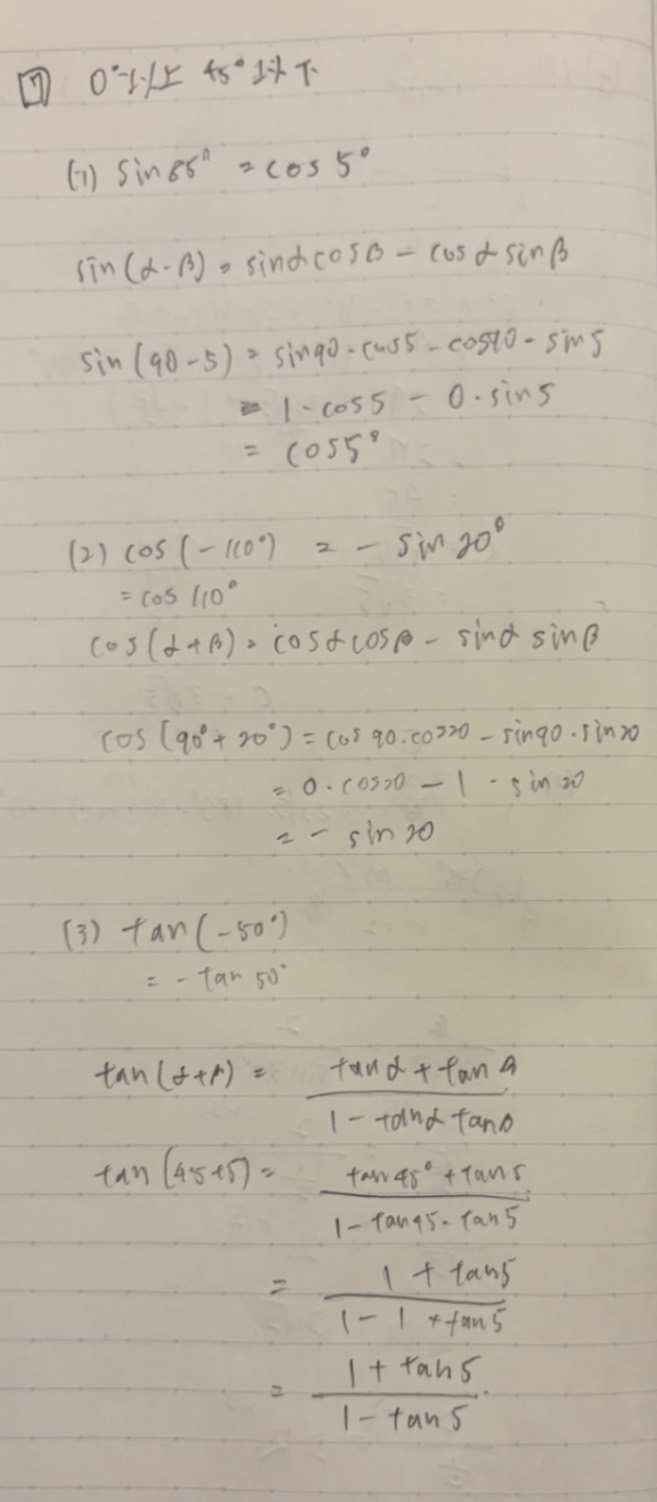

回答
くりさん 、
あれ?問題の趣旨というか使う道具を間違えていますよ。
45°以下の三角関数で表わすためには、加法定理ではなく180°ーαの変換公式や90°ーαの変換公式や90°+αの変換公式を使いますよ。
あなたのノートの各カッコの1行目が正解ですが、それは自分で出したものではないのかな?正解を写しただけなのかな?
85°=90°ー5°ですから90°ーαの変換公式
$\cos(-\theta)=\cos\theta$ という公式を知っているのなら、マイナスはなくして110°=90°+20°なので90°+αの変換公式
$\tan(-\theta)=-\tan\theta$ という公式でマイナスは前に出し、50°=90°ー40°だから90°ーαの変換公式
教科書に変換公式はのっているはずなので調べてくださいね。
このあたりはやたら公式っぽいものがたくさん出てきます。覚えなくても図を上手に書けば導けます。
これで大丈夫ですか?これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。
=================
追記
はい、(1)(2)はそれでいいですね。加法定理でやっても正解です。でも(1)では $\sin\left(\dfrac{\pi}{2} -\theta\right)=\cos\theta$ を使って
$\sin 85°=\sin(90-5)=\cos 5°$
(2)は $\cos\left(\dfrac{\pi}{2} +\theta\right)=-\sin\theta$ を使って $\cos(-110°)=\cos 110°=\cos(90°+20°)=-\sin 20°$
(3)は $\sin\left(\dfrac{\pi}{2} -\theta\right)=\cos\theta$ と$\cos\left(\dfrac{\pi}{2} -\theta\right)=\sin\theta$ を使ってやってもいいし、
$\tan\left(\dfrac{\pi}{2} -\theta\right)=\dfrac{1}{\tan\theta}$ を使ってもいいし。
$\tan -50°=-\tan 50°=-\dfrac{\sin(90°-40°)}{\cos(90°-40°)}=-\dfrac{\cos 40°}{\sin 40°}=-\dfrac{1}{\tan 40°}$
または
$\tan -50°=-\tan 50°=-\tan (90°-40°)=-\dfrac{1}{\tan 40°}$
となります。
(3)はあなたの答でも題意を満たしているので〇かもしれませんが、やはり1つの三角関数で表わした方がいいでしょう。
3枚目の写真は変換公式の1つですね。ほかにもないですか?90°+θとか180°ーθとか。
各カッコの1行目というと、cos5°や-sin20°のところでしょうか?そこでしたらその下に書いてある式で出したものなので一応正解ということにはなるのでしょうか? また、変換公式とは追加した写真3枚目のものでしょうか?tanの変換公式は載っていないのでsinやcosにどうにか直して解く形になりますか? 教えていただけると幸いです。
教科書をよく見たら数ページ先の文中にtanの変換公式もさらっと書かれていました。 加法定理より大分楽に解けました。 ありがとうございます。
それならよかったです。公式全部丸暗記というのは無理なので、作り方や単位円のずから作れるようになるの楽です。