三角関数　グラフ

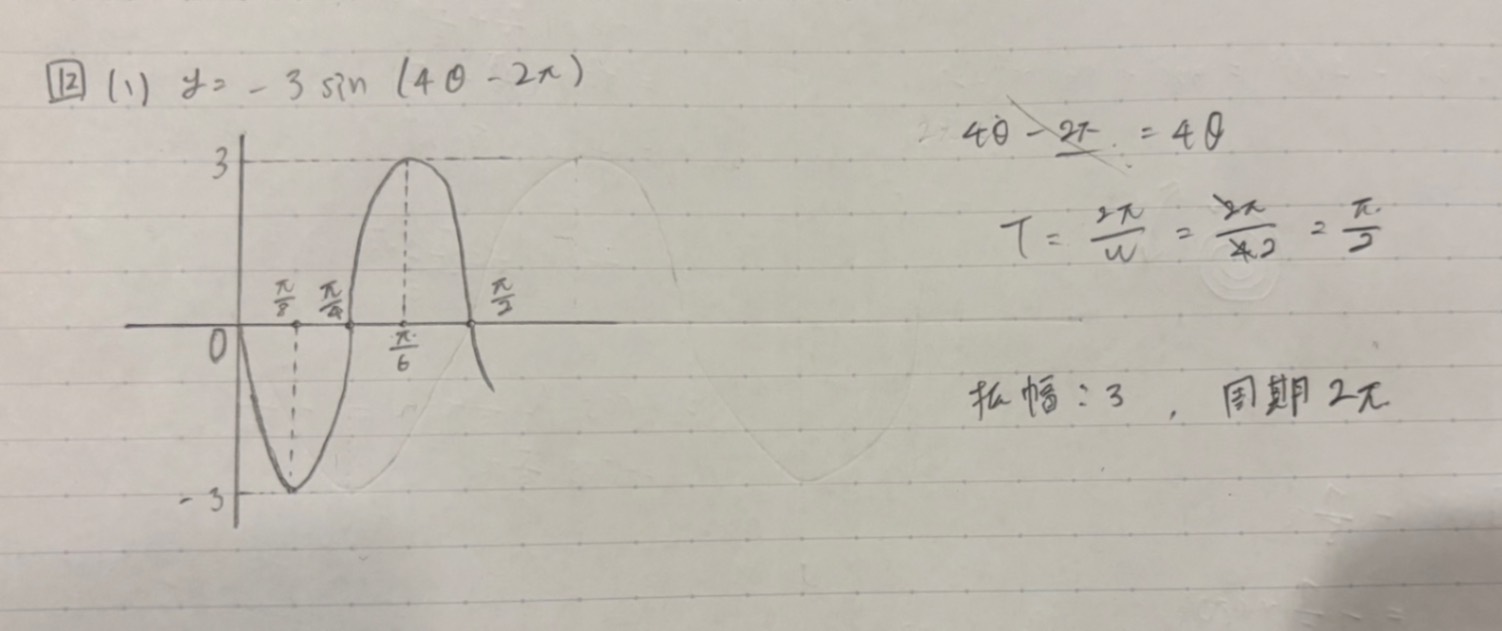
写真の問題について教えていただきたいです。 $y=-3sin(4θ-2π)$のグラフを書く問題ですが、$sin(4θ-2π)$がどういう意味なのか分かりません。 $sin(θ-\frac{π}{4}) $とかでしたらθ軸方向に$\frac{π}{4} $だけ平行移動するとわかるんですが…… ご回答よろしくお願いします。

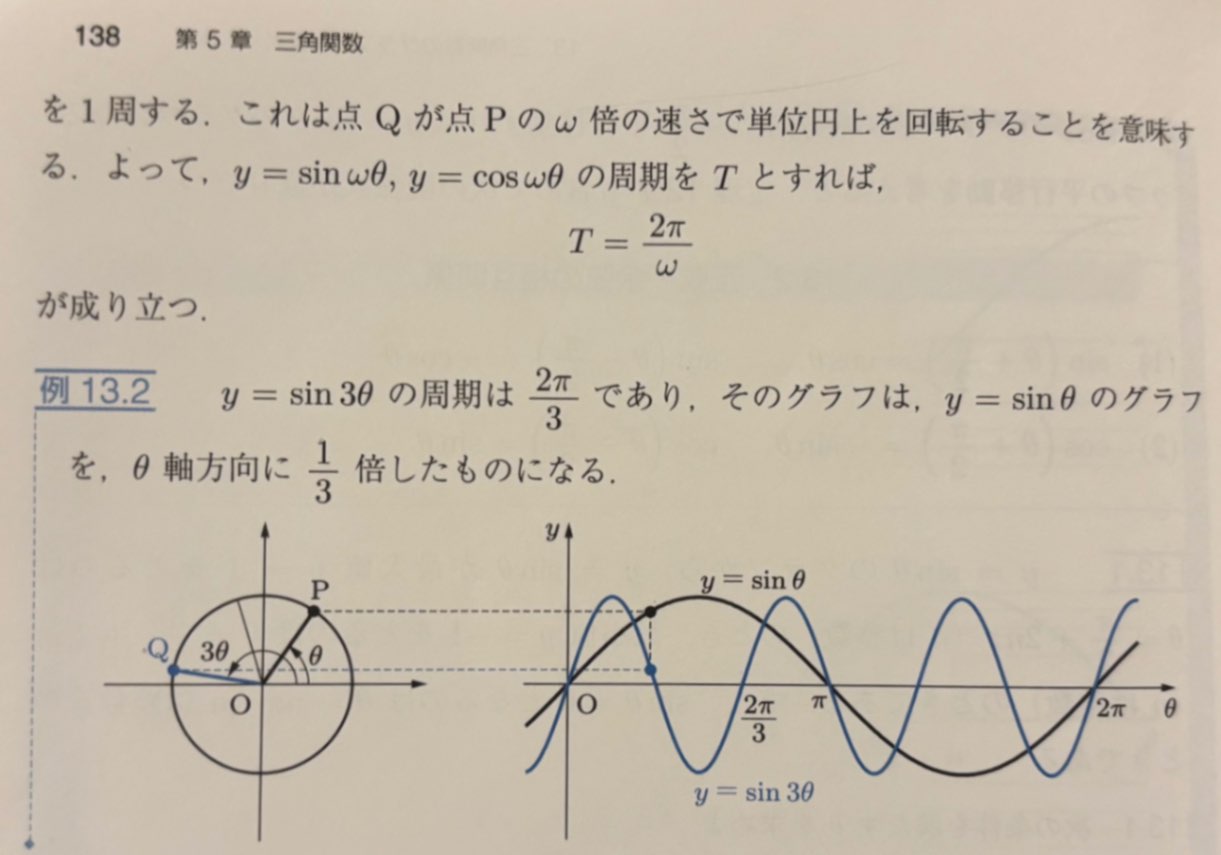
くりさん、 $y=\sin n\theta$ のグラフについてのまとめは教科書とか参考書にあると思うのですが、ないですか？ おおもとの関数は $\sin \theta$ ですね。±1の範囲で波打ち、周期は2πです。それに-3をかけたのですから、±3の振幅になり、さらにx軸に対した対称移動(裏返し)します。 次には $y=-3\sin 4\theta$ ですが、 $y=-3\sin \theta$ と形は同じですが周期が変わります。サイン関数は角が2πだけ変化すると元に戻ります。角の部分が4θのときは4θが2πだけ変化するとともに戻ります。θで考えるとθがπ/2変化すれば4θは2π変化するので、θの関数としてはθがπ/2だけ変化すると元に戻るので、周期は2πの1/4のπ/2になりますね。nθのときは周期は1/nの2π/nになります。周期が短くなるということはより激しく振動することになり、グラフはy軸方向にギュッっと縮まります。ここは大丈夫ですか？ さて、最後ですが、4θ-2πではθがどうなったのか分からないので、必ず4(θ-π/2)と変形できる(無理やり変形する！)ことから、4θのθがθ-π/2になっていることがわかりますね。ですから平行移動です。 $y=-3\sin 4\theta$ のグラフを軸方向にπ/2だけ平行移動します。これで出来上がりです。角の部分がnθ-pだったらn(θ-p/n)の形に変形してから、nθのときのグラフをx軸方向にp/nだけ平行移動するということになりますよ。わかりますか？ これで大丈夫ですか？書きすぎたかな？ この問題に限っては4θという角を2πずらしても変わらない、つまり元々 $\sin(x±2π)=\sin x$ なんだから、$-3\sin 4\theta$ のグラフを書けばよかったのですね！！