微分応用

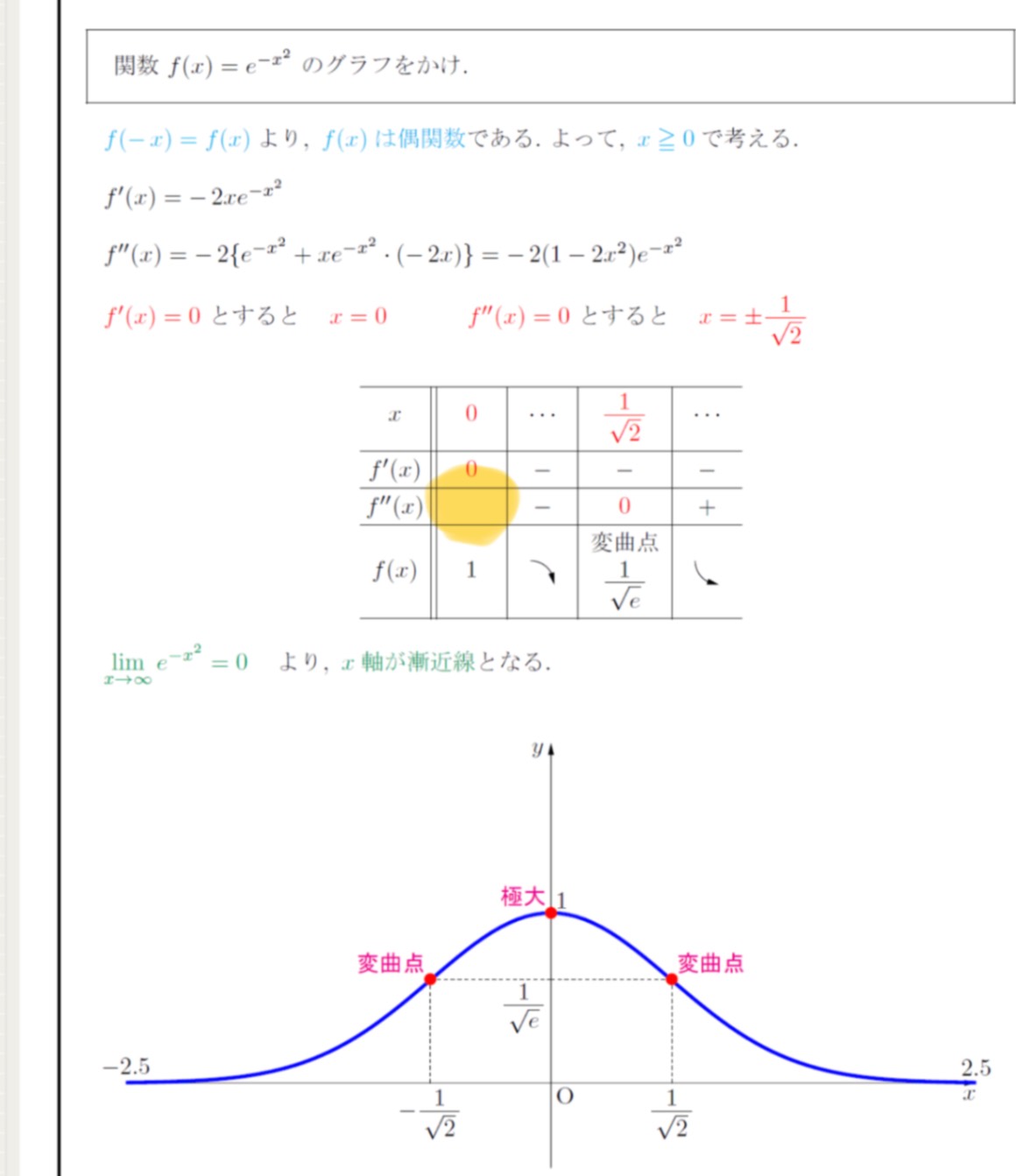
今回f(x)は偶関数なのでxがゼロ以上の時だけを考えているのですがxがゼロの時の1次導関数の符号は書いてもよろしいのでしょうか？また、黄色のところはなぜ−と書かないのでしょうか？

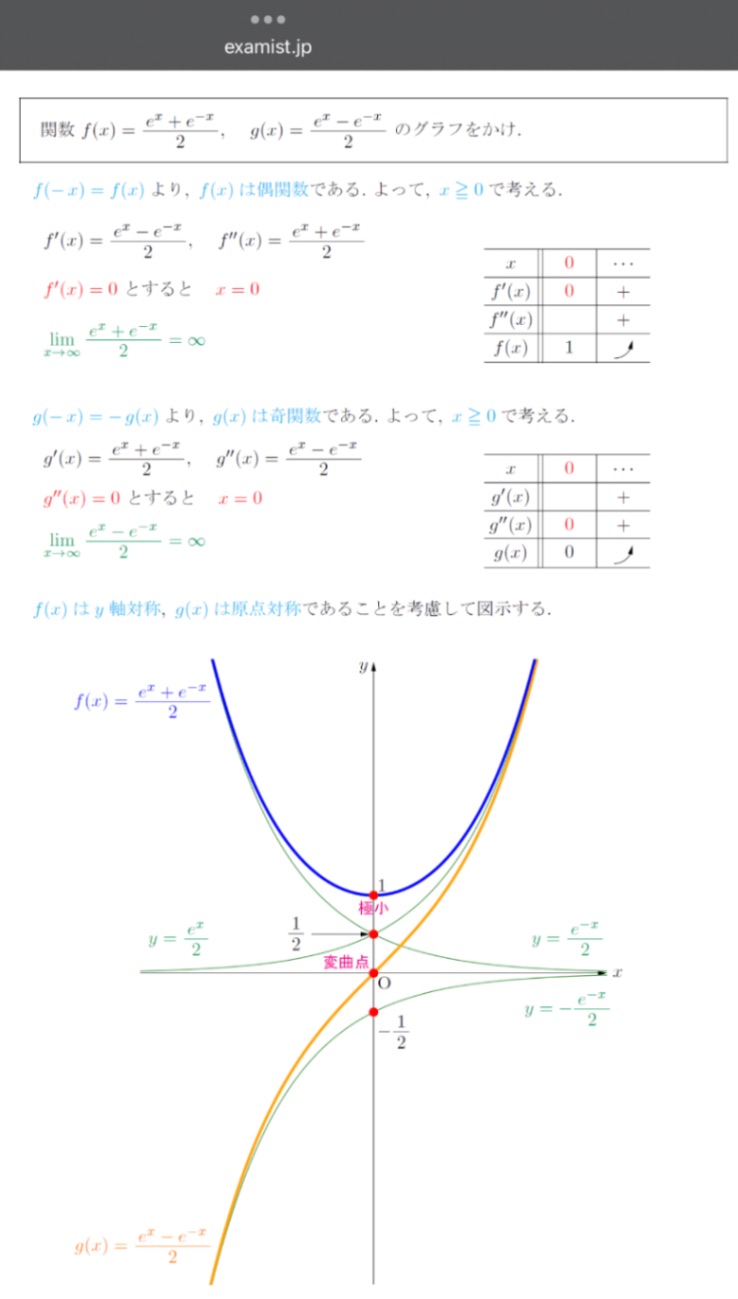
h k さん、こんにちは。 ①　f '(0)＝０ですから符号はつきません。増減表に０と書くだけですよ。 ②　黄色いところは書き忘れたんでしょうかね。書くべきですよね。 これでどうでしょうか？ ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 追記 別の問題は質問を分けてほしいのですが。 $e^{-x}$ はｘ→∞のとき、ほぼ0になるので無視すると、f(x)もg(x)も$y=\dfrac{e^x\pm 0}{2}$ になり、これが右側の漸近曲線です。 $e^x$ はｘ→ー∞のとき、ほぼ0になるので無視すると、f(x)は $y=\dfrac{0+e^{-x}}{2}$ に、g(x)は $y=\dfrac{0-e^{-x}}{2}$ になり、これらが左側の漸近曲線です。 わかりますか？