このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
二項分布
(2)についてです。
一応自力で解いたのですが、なんでこのようにしたら解けたのか自分の中でわかってません。なんとなく似たような問題で同じような解き方だったので同じようにやってみたら答えがあってしまいました、、
そもそも、二項分布に従うというところがあまりわかりません💦
二項分布とはなんなのでしょう??
よろしくお願いします🙇♀️
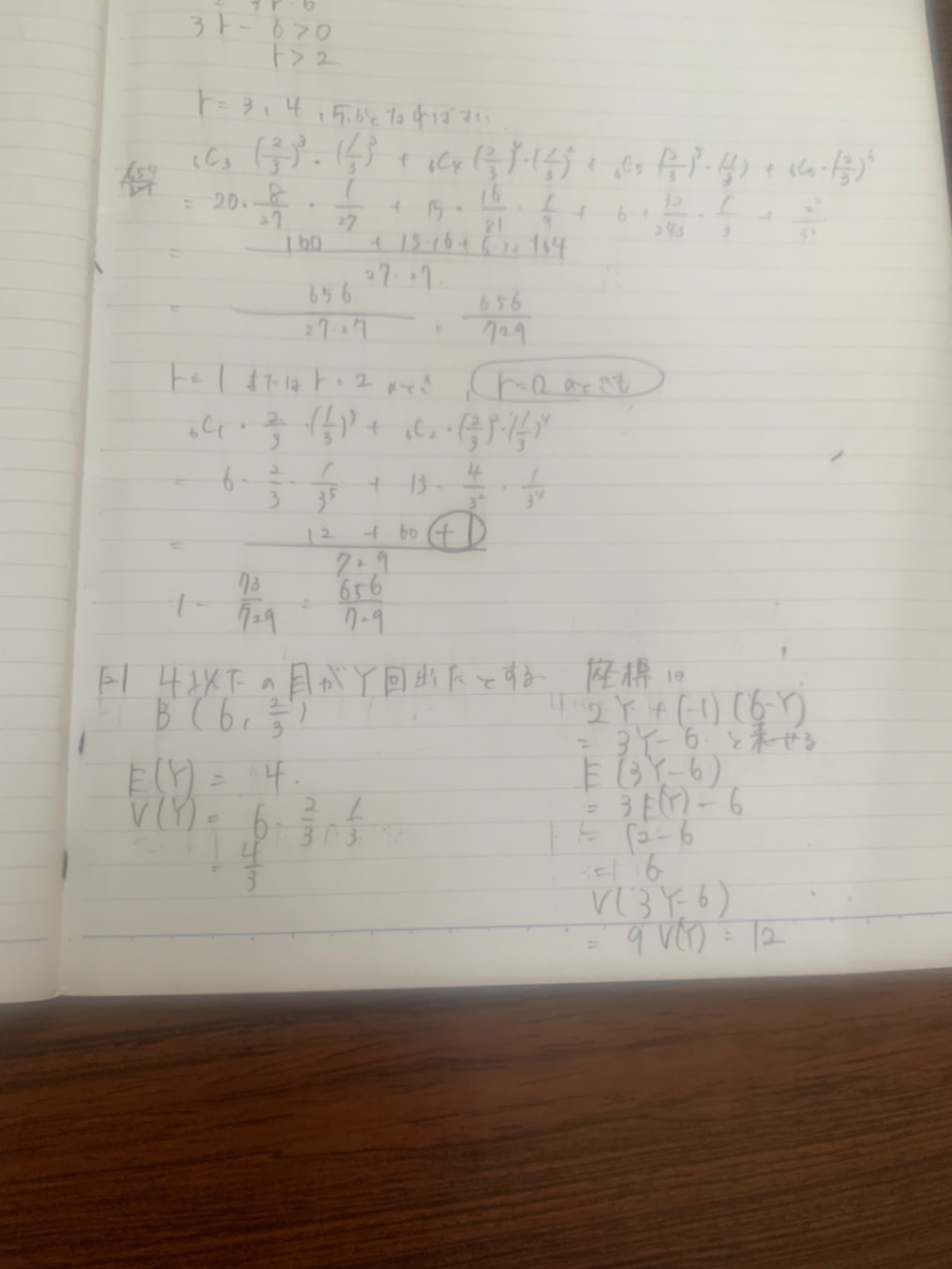

回答
百花さん、こんにちは。
二項分布全般の解説はとてもここには書けません。ネットで検索すればたくさん出てくるので、そちらを読んでください。
平たく言えば、ことがらAが起こるか起こらないかという独立な試行をn回するときの、起こる回数Yの分布を二項分布と言います。これは定義です。
なぜ二項なのかというと、Aが起こる確率をp、起こらない確率をq=1-pとしたとき、
$(p+q)^n$ を2項定理で展開した時の各項 $_nC_r p^r q^{n-r}$ (r=0,1,2,…,n-1,n)がY=rになる確率になっているからです。
(注:普通の2項展開では累乗の指数rとn-rの位置が逆ですが、これでも内容は同じです)
展開した左辺は、Yが0回からn回までのそれぞれの起きる確率の和、右辺は1のn乗で1ですから、うまくいってるでしょ?
分布というのは、試行の結果がどんな確率でばらけているか、というような意味です。
この確率変数の分布は2項分布だと分かってしまえば、あとはその平均や分散については公式を使うということになりますね。
これで大丈夫ですか?
なるほど、ありがとうございます。自分でいろんなサイト読んでみました🙇♀️ とりあえず、反復試行の時の確率分布は二項分布の公式 B( ,)という形で表すことができるということでしょうか? 全ての試行に対して確率が同じであるときに使えるということですか?
はい、事象Aが起こるか起こらないかという独立試行の反復試行で事象Aが起こる回数の分布が2項分布です。それをB(n,p)と記号で表わします。この分布は回数nと事象Aが起こる確率pだけで決まってしまいます。「全ての試行に対して確率が同じ」という意味がちょっとはっきりしないのですが「独立」「それ以前の結果に左右されない」という意味ならOKです。これで大丈夫ですか?
ありがとうございます!
どういたしまして。