直線に関する点の対象移動について

この問題について質問です。 この問題では−θ回転すれば実軸に重なるとありますが、教科書を見ると cos（−θ） +ℹ︎sin（−θ）だと原点から−θ回転したという意味になるのではないのでしょうか？ なぜ−θすると、原点から−θではなく、実軸に重なるのか教えていただきたいです。

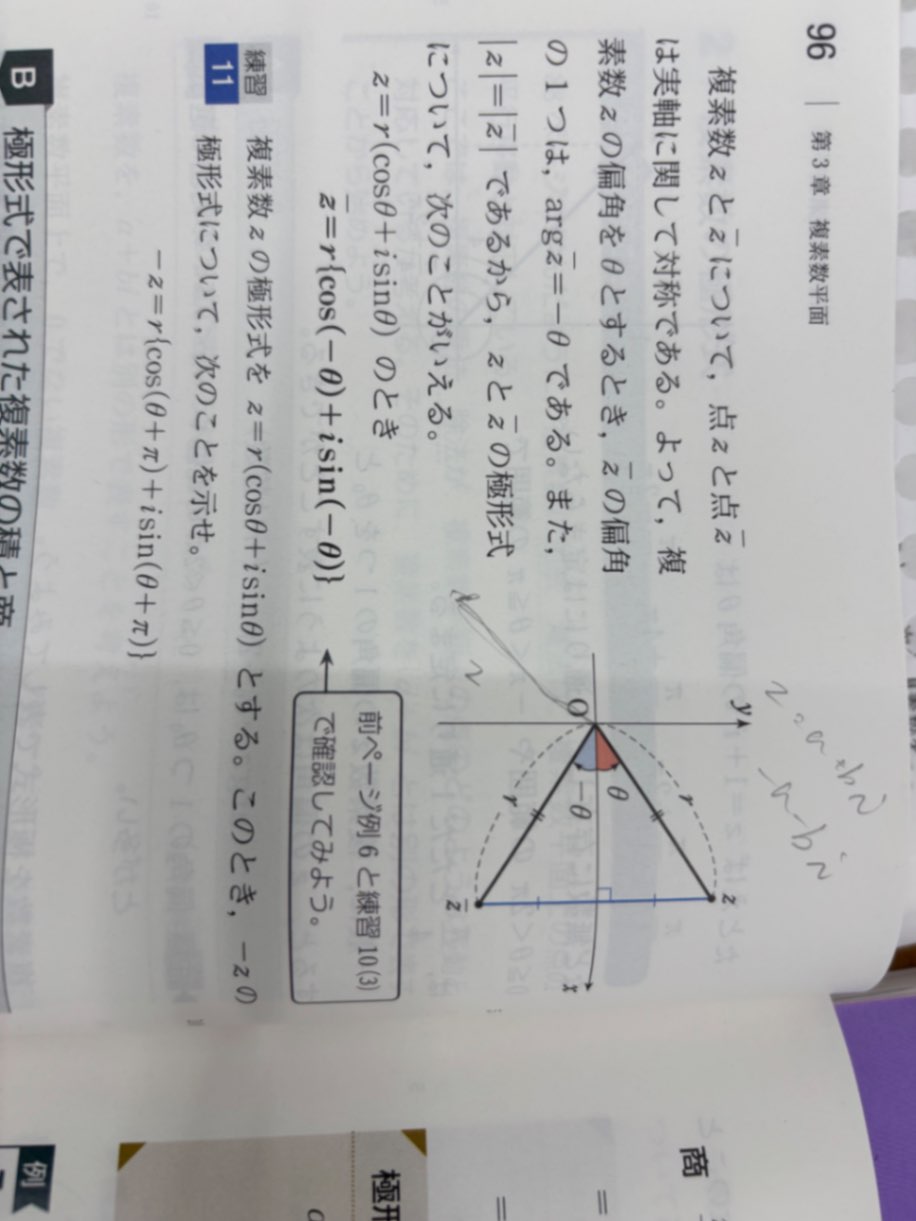
馬渕 皓士 さん、こんばんは。初めての方ですね。よろしく。 下の写真が教科書なのかな？ そこは「共役複素数は実軸に対称な点だから、偏角はーθになる」ということが書いてあるのです。回転とかではないと思います。 「複素数ｚを原点を中心にーθだけ回転した複素数ｗは $\Big(\cos(-\theta)+i\sin(-\theta)\Big)z$ 」という話とは違うようですね。 ｚをーθだけ回転したかったら $\cos(-\theta)+i\sin(-\theta)$ をかければいいということです。 質問の問題の「考え方の①」でしょうか？違っていたら言ってください。 それは「線分OAを原点Oを中心に」という目的語が抜けているので誤解しそうですが、ｚを、ではなく、線分OAを、です。 図形的に考えています。OAをーθだけ回転するとAが実軸上のA'に来て、線分OA'は実軸と重なる」と言っています。 解答の1行目は教科書の「共役複素数」と同じことです。 これで大丈夫ですか？あなたの質問に答えられていますか？ ここでは会話型を目指しています。 これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。返事がないと、せっかく書いたものを読んでくれたのかどうか、書いたものが役に立ったのかどうか、こちらではわからないのです。コメントよろしく。