文字式

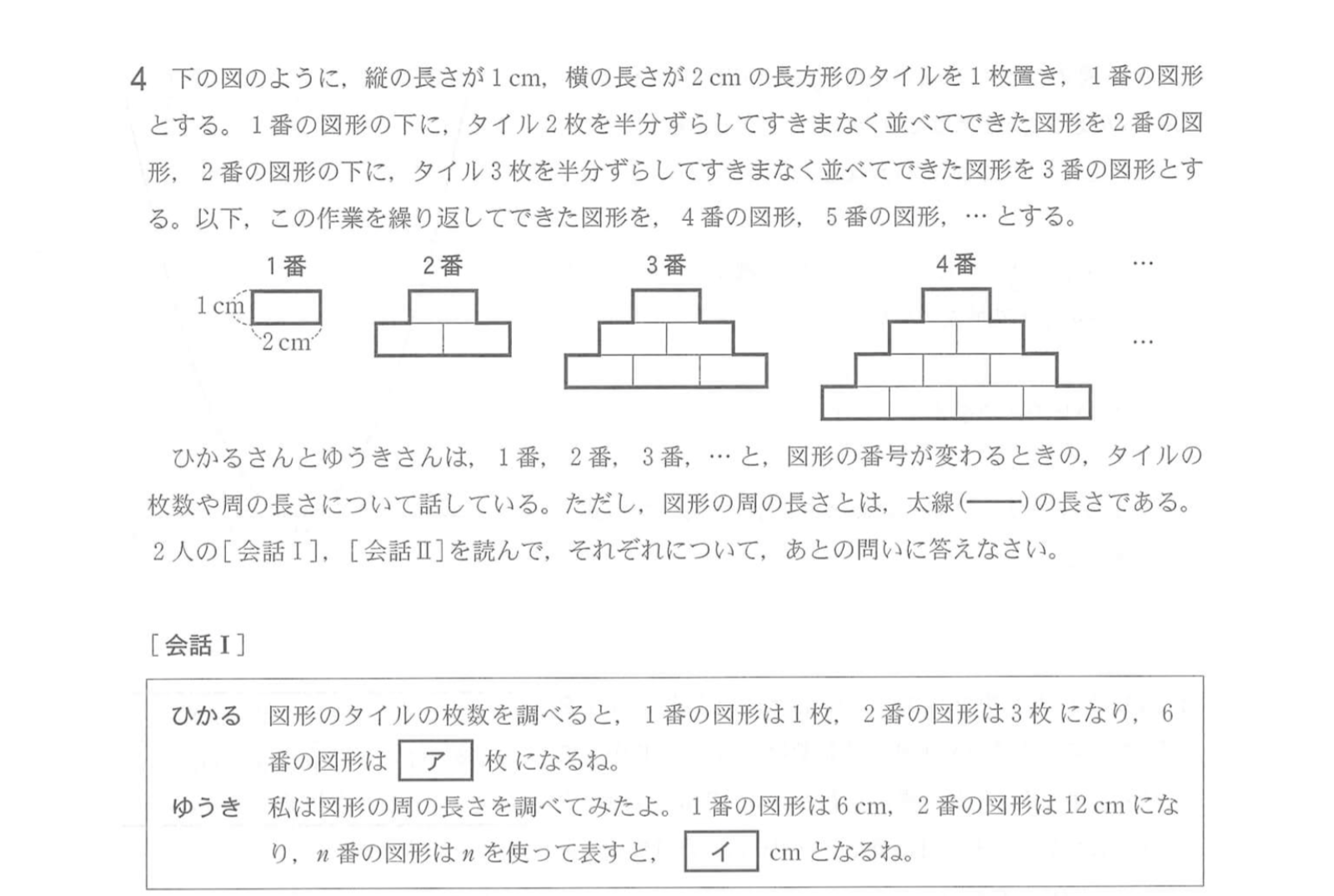
文字式の応用についてです。 (3)の質問です。 (2)のより周の長さについての式を立てることはできました。また、共通の値ということから「=」でつなぐ等式で求めればいいんじゃないかなと思いもう1つの式を立てようを考えてみたんですが、全く思いつかなくて… どのように考えれば答えがでてきますか？(答えはウ11　エ66)

楓さん、こんばんは。 う～む、中学生ですよね。どうやればいいのかなぁ。式で解こうとすると高校の知識を使うのですが…でもまぁ、知っている中学生も多いということなのかなぁ。 １＋２＋３＋…っていうふうに順に足して、ｎまで足したら和がどんな式になるのかを知っていますか？ タイルの枚数は　１、１＋２、１＋２＋３、…というふうに増えていくのです。だから上の事柄を知らないとできないかも。 https://math.nakaken88.com/textbook/basic-sum-of-n/　←ここに説明があります。難しくはないのでぜひ！！読んでください。 １からｎまでの自然数の和は $\dfrac{1}{2}n(n+1)$ という式で求められるのです。 よってｎ番目の図では、タイルの数は $\dfrac{1}{2}n(n+1)$ 枚、周の長さは６ｎｃｍ。これが等しいようなｎを求めれば、それがウになりますよ。ｎについての2次方程式を解くことになります。 これで大丈夫ですか？ この公式は絶対覚えた方がいいです。 １から１０までの和は？１０×１１÷２＝５５ １から１０００までの和は？１０００×１００１÷2＝５０５００ １から３５７までの和は？３５７×３５８÷2＝６３９０３ というふうに、足し算しなくても求められるのです。便利です！