文字式2

文字式です。 (3)の考え方の流れは頭で組み立ててみたのですが途中からよくわからなくなってしましました。考え方としてはn番目の時のひとマスのときにn²になるから、それを使って求めてみよう！という感じでした。 なんですか、わかりません。

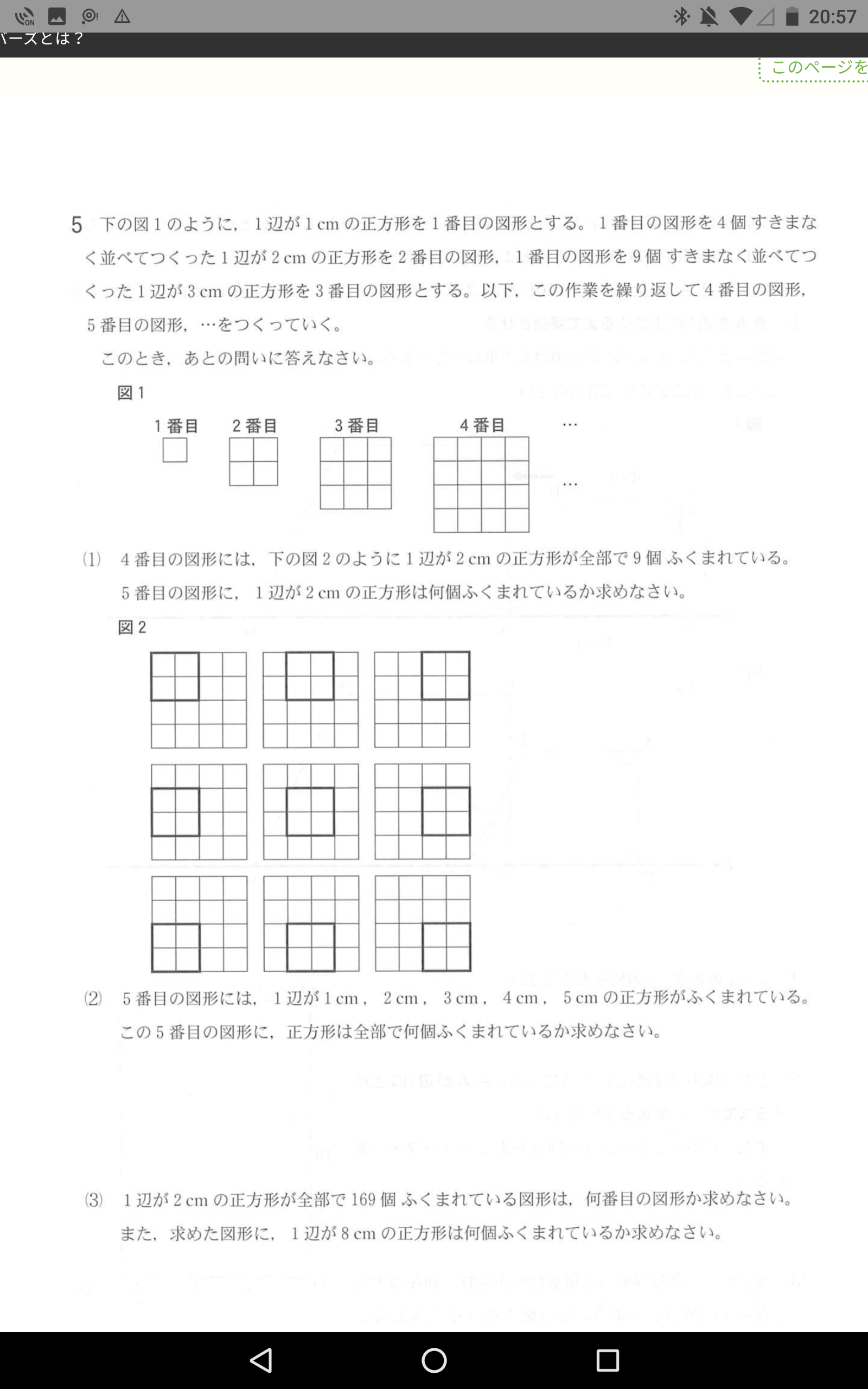
楓さん、 ｎ番目の図形に２ｃｍの正方形がいくつ入っているかを計算する方法は分かってますか？ 縦横にｎ＋１本ずつ線があって、縦線で２ｃｍ離れた２本と、横線でも２ｃｍ離れた２本を選ぶと２ｃｍの正方形が１個決まります。 じゃ、その決め方は？ 縦線ｎ＋１本で、２ｃｍ離れた２本の選び方はｎ－１通りあるのはわかりますか？具体的に５番目とか７番目とかで確かめてみてください。２ｃｍ離れた縦線２本の選び方です。一番左のと左から３番目が見つかって、あとはそれを１ｃｍずつ右に動かしていけば、５番目の図形では４とおり、７番目の図形では６通り選べますね。 縦線の選び方はｎ－１通り。同じく横線でも２ｃｍ離れた２本の線の選び方はｎ－１通りです。よって縦横２ｃｍずつ離れた４本の選び方は $(n-1)^2$ 通りになります。わかりますか？ということは２ｃｍの正方形が $(n-1)^2$ 個あるということです！ で（３）です。１６９が１３の２乗であることを見抜かなくてはならないのです。 １３²＝１６９です。$(n-1)^2=169$ です。よってｎ－１＝１３なのでｎ＝１４となります。つまり１４番目の図形。 じゃ、８ｃｍの正方形は、縦横それぞれ１５本のうちで８ｃｍ離れた２本の線が何通りあるかを調べていけば、２ｃｍのときと同じようにして分かります。これはまだ種明かしはしませんから、考えてみてくださいね。 これで大丈夫ですか？コメント欄になにか返事を書いてください。