共テ数学

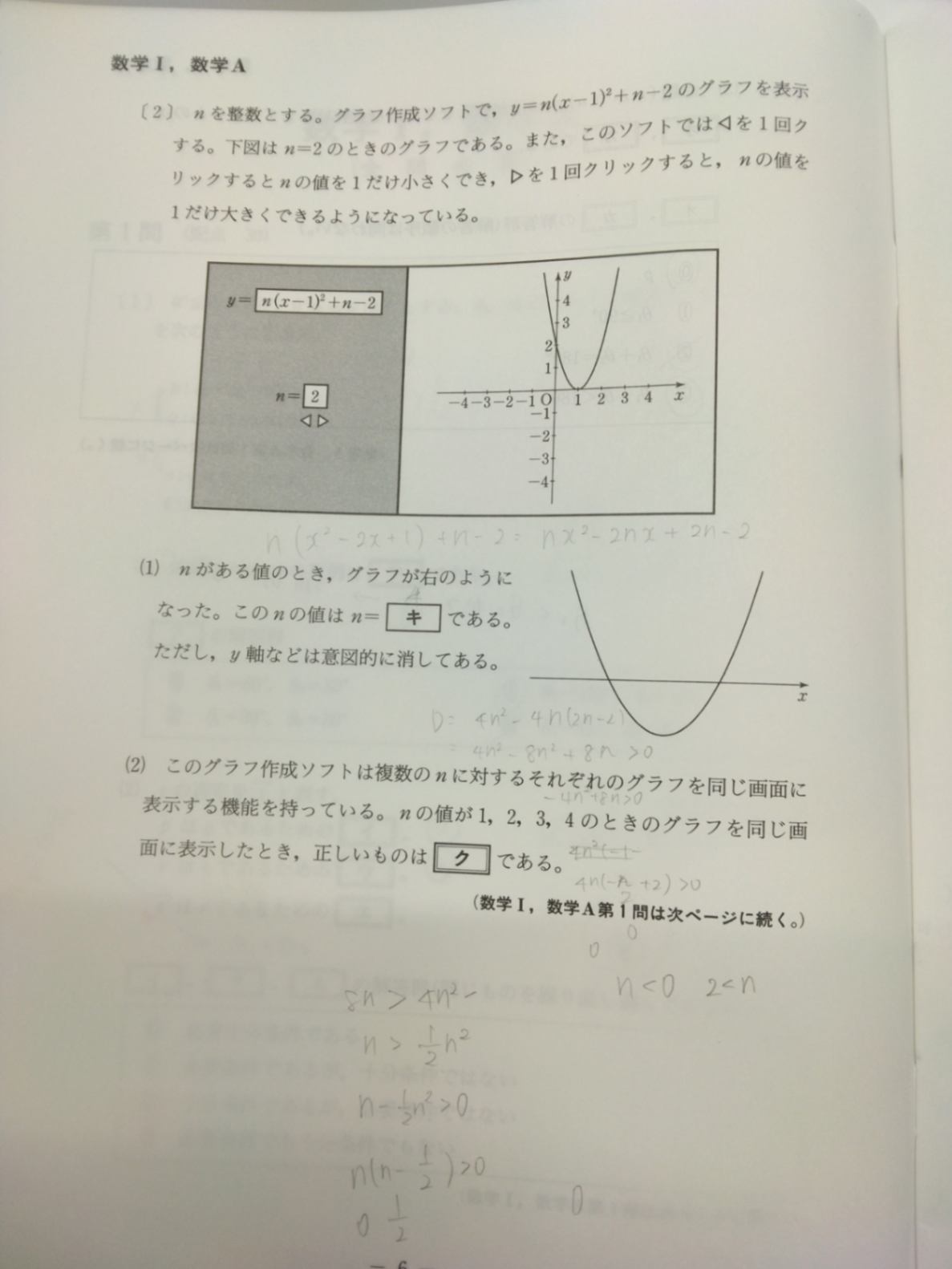
(キ)がわかりません。 判別式が0以上のことを使ったのですが、n＜0、2＜nになってしまいました。何がおかしいのでしょうか

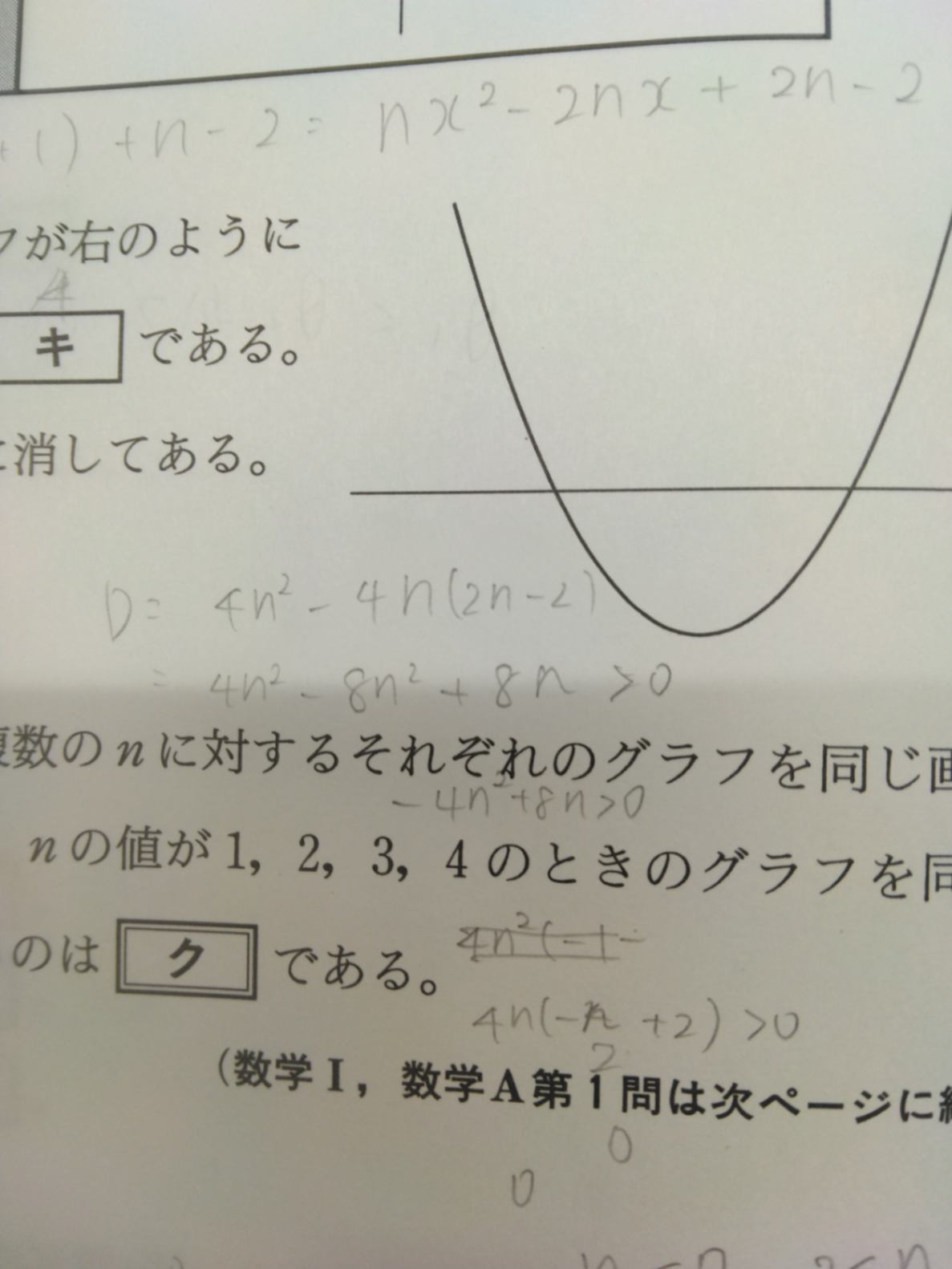
忠さん、こんにちは。 ２枚目の写真が判別式を使ったところですね。 あ～！おしいですが違ってます。最後の最後で！ 2次不等式で…＞０の時は２解の外側、と丸暗記してますね。しかしこのことがらには条件が付いていて「２乗の係数が正のとき」しか使えません。 今解こうとしているｎの２次不等式の２乗の係数は負になります。ですから逆に「２解のあいだ」になるのです。それは２次関数のグラフが上に凸になるからです。 しかし、原則は「２次不等式を解くときは、まず２次の係数を正にしてから考える」です。 ー４ｎ²＋８ｎ＞０は両辺にー１をかけて　４ｎ²－８ｎ＜０にしてから解きましょう！その方が間違いが少ないです。 ◎２次不等式の２乗の係数はプラスにする！！！ そうすれば…＞０なら２解の外側、…＜０なら２解のあいだ、という覚え方で大丈夫なんです。 これでいいですか？ ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 追記 いま考えたら、もっと単純な問題みたい。 図のようになるのだから２乗の係数は正、つまりｎ＞０。 また頂点がⅹ軸より下なのだからのｙ座標が負、すなわちｎ－２＜０。よってｎ＜２。 以上より０＜ｎ＜２だからｎ＝１。 これでいいみたい。

髙木 忠 さん、こんにちは。 $1$ 枚目の写真の $n-\dfrac{1}{2}n^2 > 0$ という式は正しいですが、その直後の $n$ でくくる操作で計算ミスをしています。 正しい計算は次のようになります。 $n-\dfrac{1}{2}n^2 > 0$ 左辺を $n$ でくくると、 $n\left(1-\dfrac{1}{2}n\right) > 0$ 括弧の中の $n$ の係数を正にするため、両辺を $-1$ 倍して不等号の向きを逆にします。 $n\left(\dfrac{1}{2}n-1\right) < 0$ この二次不等式を解くと、$0 < n < 2$ となります。 なお、$8n > 4n^2$ の段階で両辺を $8$ ではなく $4$ で割ると分数が現れずに計算が簡単になります。 $4$ で割ると、$2n > n^2$ となり、これを解いても、$0 < n < 2$ という同じ結果が得られます。 ご不明な点があれば、お気軽にコメントでご質問ください。