このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
2字曲線と軌跡
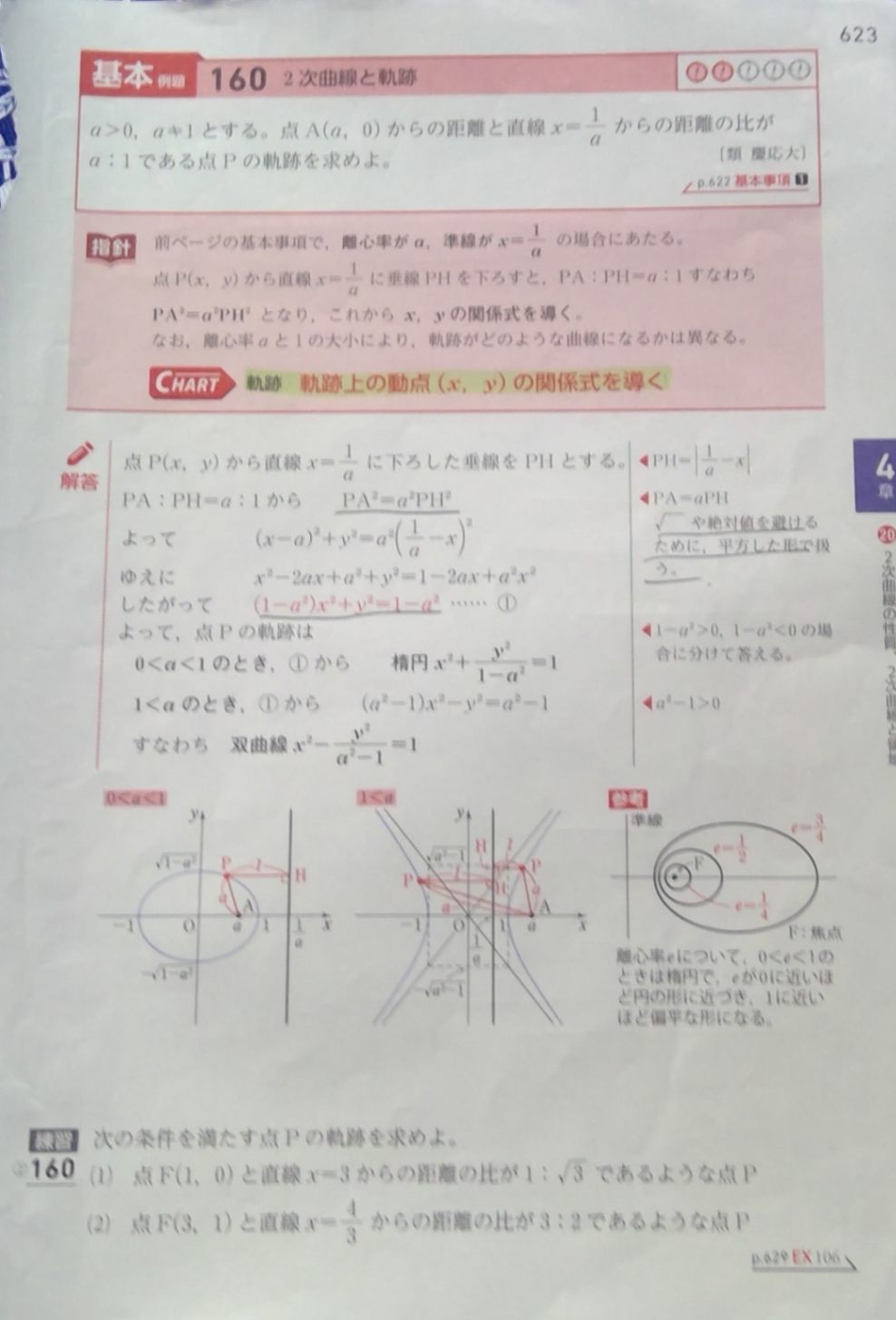
〇C 160
最後、場合分けしているのは、楕円のY^2の部分の分母が負になってはいけないからですか?
回答
北大 受かりたい さん、
場合分けする理由ですね。
一般に $Ax^2+By^2=c$ という形の式で表わされる図形は2次曲線になります。ときには例外もあって2本の直線になったり1本の直線になったりなにも表わさなかったりすることもありますが、それは例外ということで、一般には2次曲線=放物線、楕円(円も含めて)、双曲線です。
その3つに分かれるので、解答の①式で「2次曲線だ!」ということは分かりましたが、放物線、楕円(円も含めて)、双曲線のどれなのかは係数次第なのです。それでしょうがないので場合分けをしましたよ。
$Ax^2+By^2=c$ という形の式では、A,B,Cが同符号なら楕円、異符号が混じっていれば双曲線。AかBが0なら放物線みたいに判別できます(ちょっと荒っぽいです。厳密ではありません)。
この問題ではy²の係数は+1が分かっているので、x²の係数の正負で場合を分けました。
問題にa≠1と書いてあるので、分母が0になることはありません。
これで大丈夫ですか?
なるほど...! そこまで体系化して考えれていませんでした...。 くさぼうぼうさんのお返事の11-13行目について、厳密ではないということはたまに例外があるということですか...?
あ、いや、もっと細かい場合分けが必要なものも省略しているので… なお、行数で言われても、デバイスによって異なってしまいます。
Ax^2+By ^2=c という形の式では、A,B,Cが同符号なら楕円、異符号が混じっていれば双曲線。AかBが0なら放物線みたいに判別できます(ちょっと荒っぽいです。厳密ではありません) というところの話をしていたつもりでした💦すみません。
はい、そこのつもりでお答えしました。A,B,Cの正負、0の組み合わせでどんな図形になるか系統的に調べてみることをお勧めします。2直線になったり、何も表さなかったりとは、どんな条件なのか分かると、また楽しいですよ。一つの形式で色々なものが出てきますよ!