このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
解説
どのように増えるかなどはわかったんですが式を立てるまでがどのようにすればいいかわかりません。(下の大問です。)
またこのような文字式を使った問題の解き方のコツなどあれば教えてください。

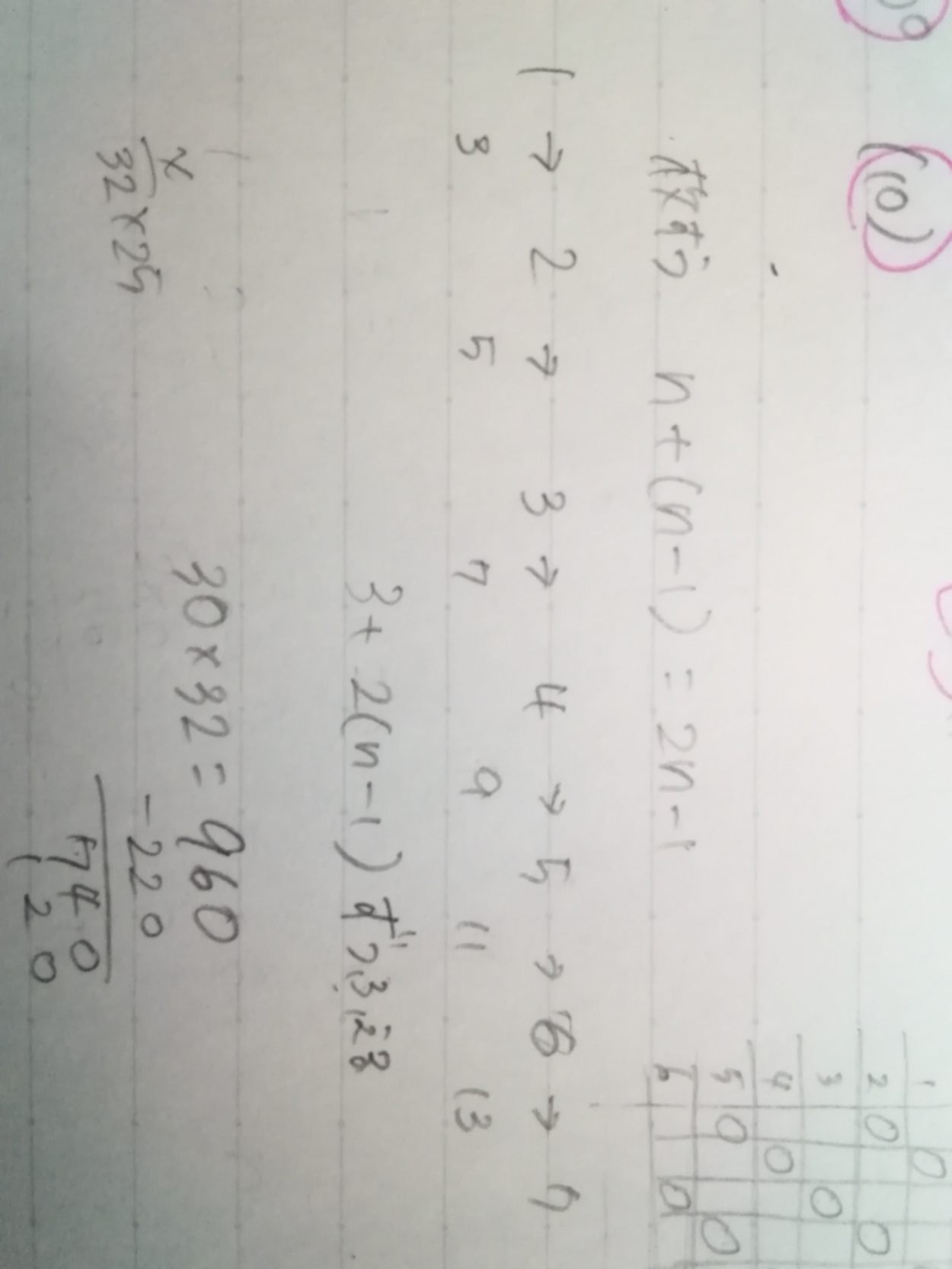

回答
楓さん、こんばんは。
こういうのは、中学の数学の範囲では、ちゃんと式を立てて計算で求めることはできないと思います。解答解説は持っていないのですか?
高校の数学では楽に解けるのですが…
たぶん、きちんとした説明や式は求められていないのでは?
この図をよ~く見て、いろいろなことに気付いてほしいというのが出題の意図だと思います。
とりあえず、段の数を2乗した数と右端の数の関係を見つけておいてください。
それと、2段目までに並んだカードの合計数、3段目までに並んだカードの合計数、4段目…というのも調べてみて、特徴をつかんでおいてください。
もう遅いので、細かい説明は明日書きます。ゴメン!
特徴を掴むことはできました! 解説なんですが答えしか載っていなくて…すみません。
もうKawai さんが、下の回答で種明かしをしてくれたので大丈夫ですね。 この手の問題は、この前の質問の問題のように、なにか発想力を試される問題のようで、きちんと式で表そうとするより、いくつか調べたりして、法則性を見抜くことが必要みたいです。
前回の時の「1+2+3+…+n=n(n+1)/2」という知識に加えて、この問題では「1から順に奇数を足すと、和は平方数になる」といのも豆知識として覚えておくといいことがあるかもしれません。 1=1² 1+3=4=2² 1+3+5=9=3² 1+3+5+7=16=4² … 1+3+…+(2n-1)=n²
レベルが高くて手こずります… いろいろな問題を解いて解き方を身につけらるしかないですね。
10の次の数字を1に戻さずに11,12・・・というように続けて行くことにします。一の位だけ見れば、元のカードの数になってます。
1
2,3,4
5,6,7,8,9
10,11,12,13,14,15,16
・・・
この時、右端は段の数の平方数になっていますよね。
そうすると、
(1)は7^2で49枚。カードに書かれた数は一の位を見れば良くて9と分かります。
(2)は14^2=196より14段目と分かります。
(3)は、カードに書かれている数は一の位の数なのですから、1桁の数の二乗を見ていけば良いのです。
0^2=0、1^2=1、2^2=4、3^2=9、4^2=16、5^2=25、6^2=36、7^2=49、8^2=64、9^2=81
一の位で出ていない数は2,3,7,8。
したがって2,3,7,8と分かります。
説明通り解いてみたら分かりました! ありがとうございます。