微分

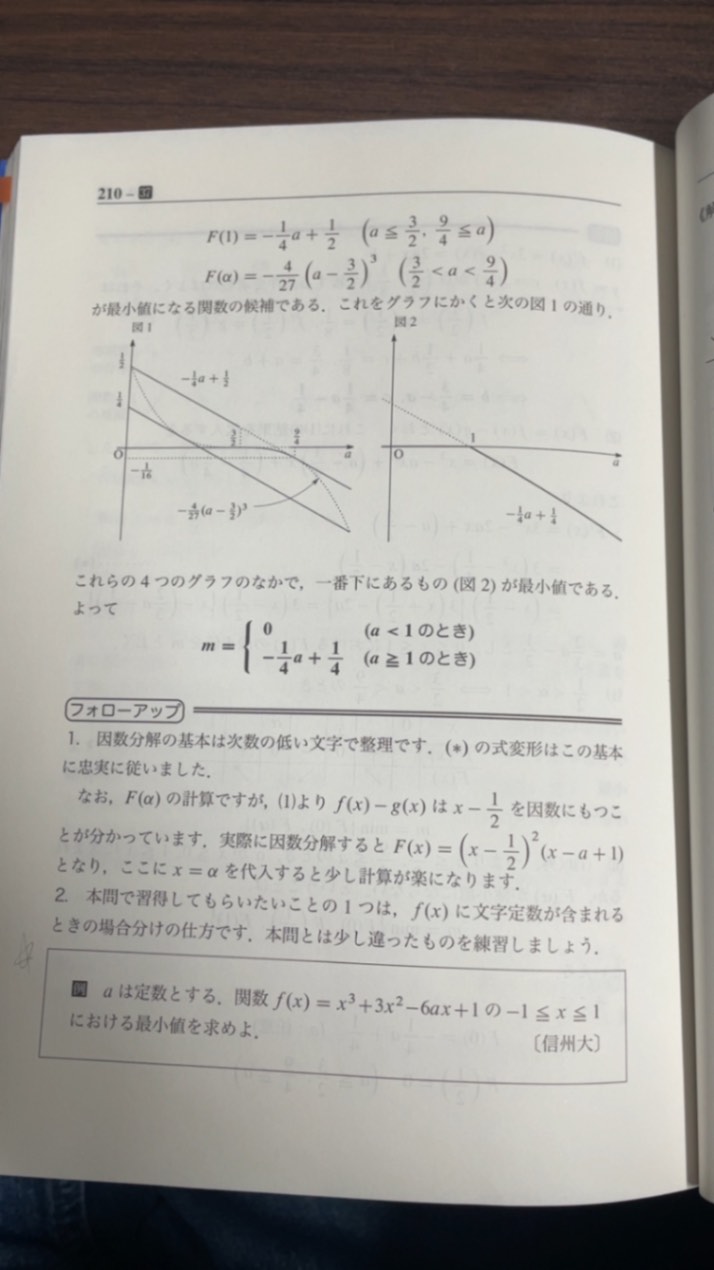
2枚目の写真についてですが、minを使うときに、問題によってはx=1/2が最小を取らない範囲なのにこうやってまとめることによって最小とみなしてしまうといったことが起こり得そうなのですが、どうやってその範囲を見分ければいいのでしょうか？

咲斗さん、こんにちは。 ひょっとして4枚目の写真？ 2枚目の写真にはminは使ってないですが。 なるほど、この解答、解法はスタンダードではないと思います。よほど慣れている人ならいいのかもしれませんが。 模範解答を書く人は慣れているのでしょう。 「…起こり得そうなのですが、どうやってその範囲を見分ければ…」と心配ですよね。 このような場合分けを使い慣れていない人が多いと思います。 私は普通にαがどこにいるか、で場合分けをするのをお勧めします。 境目が０、1/2、１なので場合分けは4つ。 場合の数が増えるかもしれませんが、このほうが具体的で図や増減表も書きやすく、最小値を撮りそうな場所2カ所も見えます。どうせf(0),f(1/2),f(1),f(α)はどこかで計算して大小を比べざるを得ないので、普通にやるほうがいいと思うのですが。 あなたの質問の直接な回答になりませんでしたが、min{ }の中に3つ入れるのは無駄です。 これで大丈夫ですか？コメント欄になにか返事を書いてください。