このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
組み合わせ
お世話になります。受験する学校の過去問を問いております。組み合わせの問題につまづいております。
問5(2)の問題です。5人の中から4人を選ぶ組み合わせまではわかりました。その宛名と書面が食い違ってる場合の数が9通りで、答えは45通りになるのですが、私は12通りと考えてしまっております。どうして9通りなのでしょうか?ここの理解ができずにおり、ご教授をお願いしたいです。
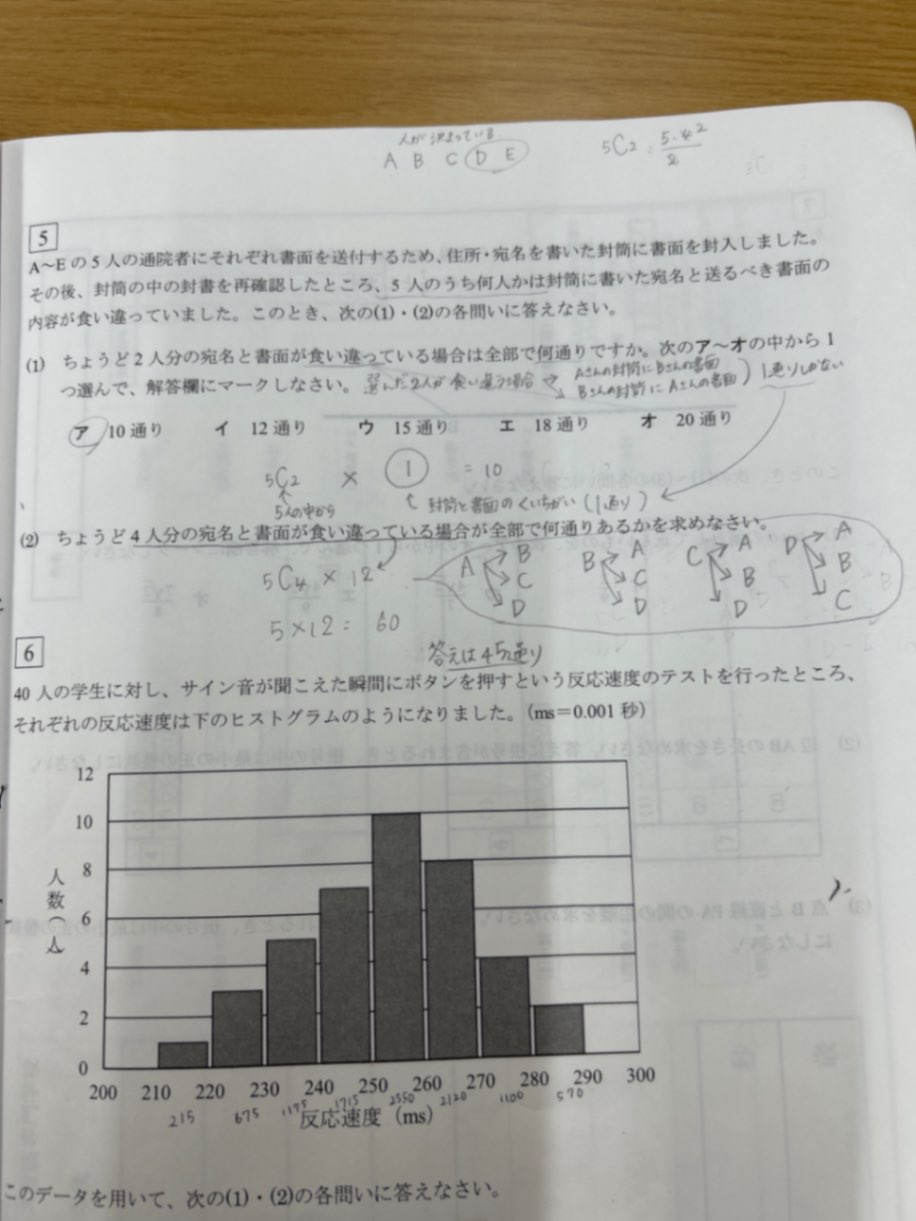
回答
ごまちゃん、こんばんは。回答が遅くなってスミマセン。
あなたが書いた樹形図のようなものほど単純ではありません。
A→B、B→C、C→A だったら、Dの行くところがなくなるのです。
A→B、B→AだったらC→AとかC→Bとかはありえず、C→D、D→Cしかないのです。
その図にはそういうものが含まれています。
A,B,C,Dそれぞれを別に考えるわけにはいかないのです。前の3つの入り方によっては最後のものの行くところがなくなってしまいます。
このように「1,2,3…を並べ替えたとき、すべてが元の番号のところにない順列」は「完全順列」という名前があって(ネットで検索すれば詳しく出てきます)、一般に、求めるのは大変難しいものなのです。このような試験で4つのものの完全順列は計算ではできません(もちろん高度な公式があることはあるのですが、たいていの人は覚えてないし、その場で作るのは困難です)。すべて書き出してみるしかないのです。
A→B、B→A、C→D、D→C
A→B、B→C、C→D、D→A
A→B、B→D、D→C、C→A
A→C、C→A、B→D、D→B
A→C、C→B、B→D、D→A
A→C、C→D、D→B、B→A
A→D、D→A、B→C、C→B
A→D、D→B、B→C、C→A
A→D、D→C、C→B、B→A
これだけです。
気合を入れて、順に考えていくしかないのです。
あまり気にするような問題ではありません。2度と出ないでしょう(笑)。無視しましょう。
教訓としては、「すべて書き出すしか方法がないことだってある!」ということです。
これでどうでしょうか?
ありがとうございます! ネットでも調べたんですけど、意味がどうしてもわからなくて、こちらの門をたたきました。とりあえず、こちらの完全順列がでましたら1番最後に回して根性で書き出してみます。 いつもありがとうございます!
👏👏どういたしまして!