このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
組み合わせの式変形について
質問失礼します。文系の大学3年生です。最近訳あって大学の微積の教科書を読み始めました。高校数学の知識すらうろ覚えの状態です。
教科書によると画像のように式変形できるようなのですが、納得がいきません。
n!と1/(n-k)!が影響しあってn・(n-1)・(n-2)・...・(n-k-1)が出てきたのだろうな思ったのですが、そこで詰まってしまいました。
どなたか詳細な計算過程を示してくださると幸いです。。
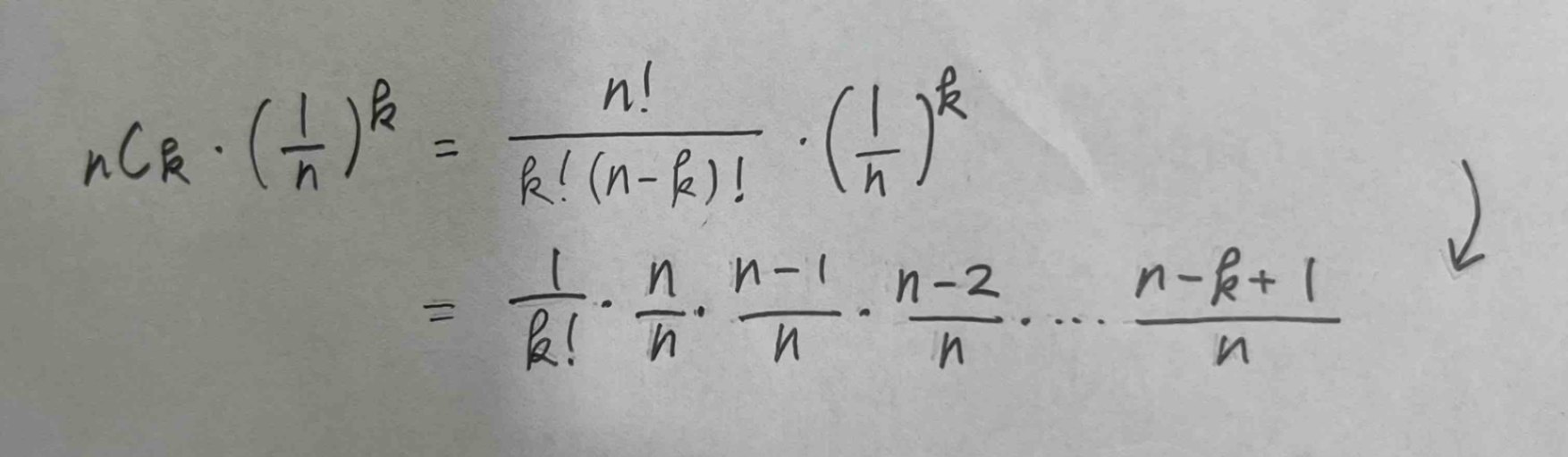
回答
なすび 大明神 さん、こんにちは。はじめてのかたですね。よろしく。なにか拝みたくなるようなお名前ですね!
あなたの考えでほぼ終わりです。あ、質問文のn-k-1はn-k+1の間違いですね。
$\dfrac{1}{k!}$ は別にして先頭に出していますから、それはいいかな?
次、n!と(n-k)!との約分で、分子にn(n-1)(n-2)...…(n-k+1) が残ります。これは全部でk個あります。そこは大丈夫ですか?
さて、$\left(\dfrac{1}{n}\right)^k=\dfrac{1}{n^k}=\dfrac{1}{nnnn\cdots}$ となって、分母にnがk個くることになります。
これで分母のn1個に分子の因数の1個を割り当てて1個ずつの分数にしていけば、結論のような式になりますね。
これで大丈夫ですか?
ここでは会話型を目指しています。これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。返事がないと、せっかく書いたものを読んでくれたのかどうか、書いたものが役に立ったのか、こちらではわからないのです。コメントよろしく。
数学、がんばってください。