このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
極限の計算
解答はlog(1+x)/xが1になるやつ使ってて、自分はlim[x→∞](1±x)^(1/x)=eを使ったんですけど、自分のやり方は❌ですか?
解答のやり方に移行した方がいいですか?

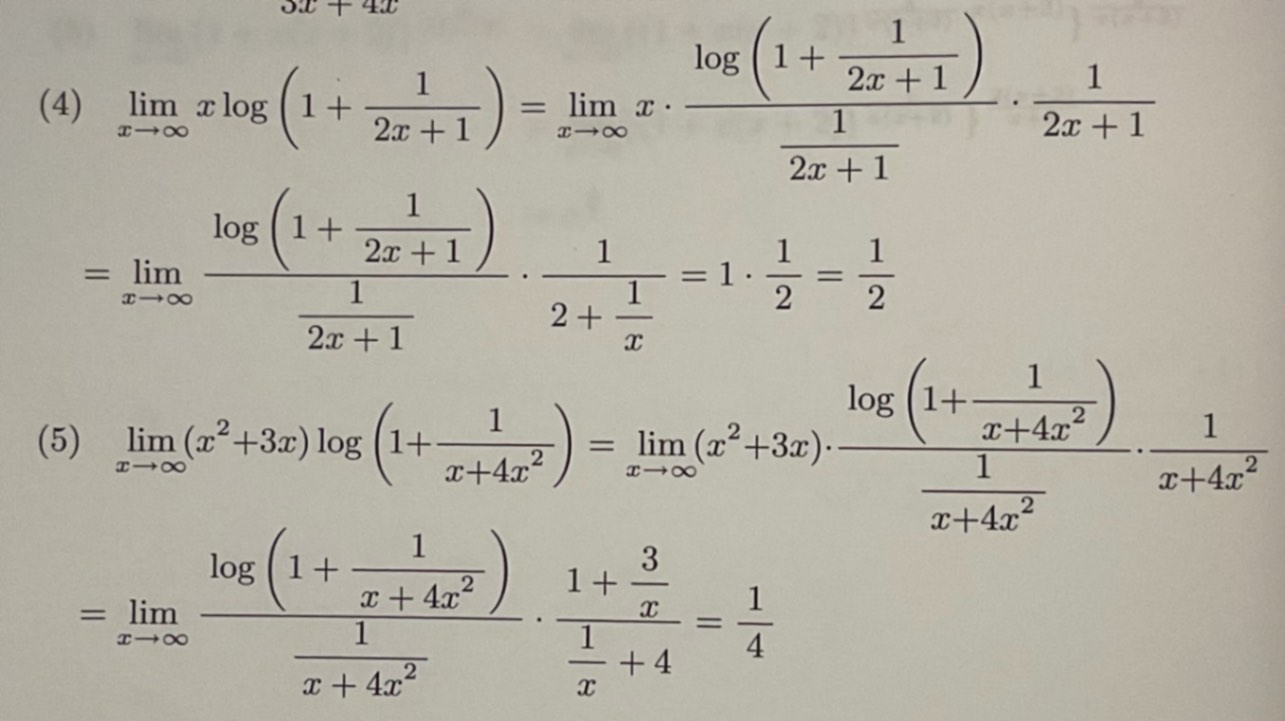
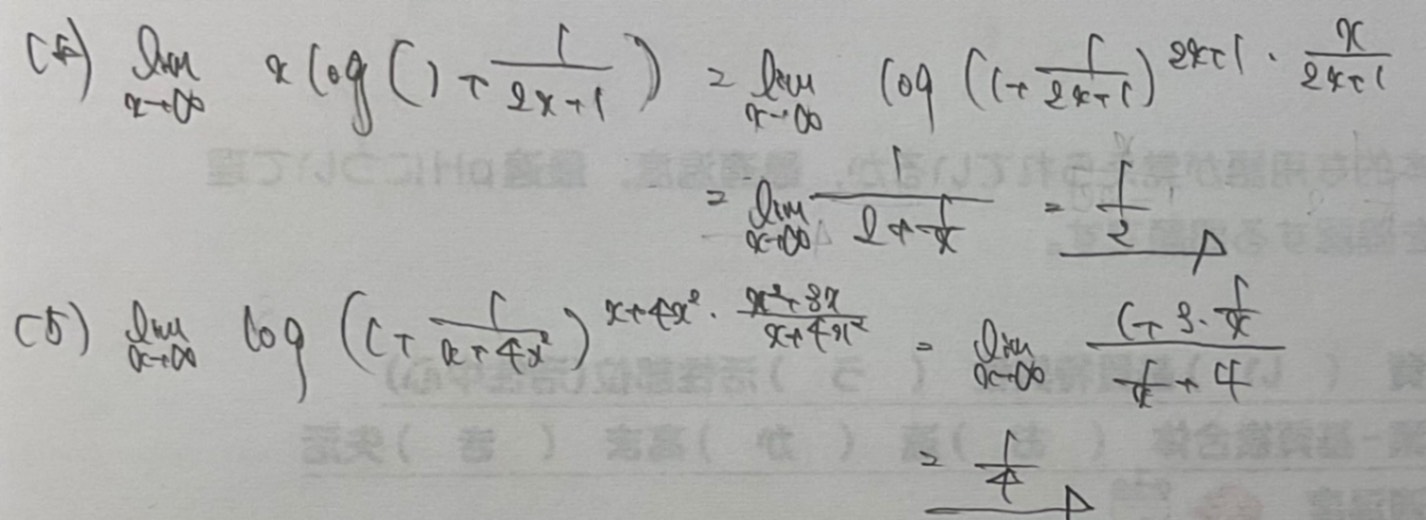
回答
ゔ ぁ さん、
問題ないと思いますよ。
ただ、あなたの答案では、どのようなことがらを使っているのか明示されていないので、ちょっと書き加えた方がいいと思います。
$=\lim_{x\to \infty }\dfrac{x}{2x+1} \log \left(1+\frac{1}{2x+1}\right) ^{2x+1}$
$=\lim_{x\to \infty }\dfrac{1}{2+\frac{1}{x}}\log \left(1+\frac{1}{2x+1}\right) ^{2x+1}$
$=\dfrac{1}{2}\cdot \log e$
$=\dfrac{1}{2}$
これはだいぶていねいな書き方ですが、参考にしてください。
これで大丈夫ですか?コメント欄になにか返事を書いてください。
それはそうと、前の2つの質問にも回答を書いたのですが、読んでないのかな?
ぜひ読んで、なにか返事を書いてください。
了解です。ありがとうございます 自分あんま理解力無いので返答に時間がかかっちゃいます 不快に思われたらすみません