このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
証明のおまけ
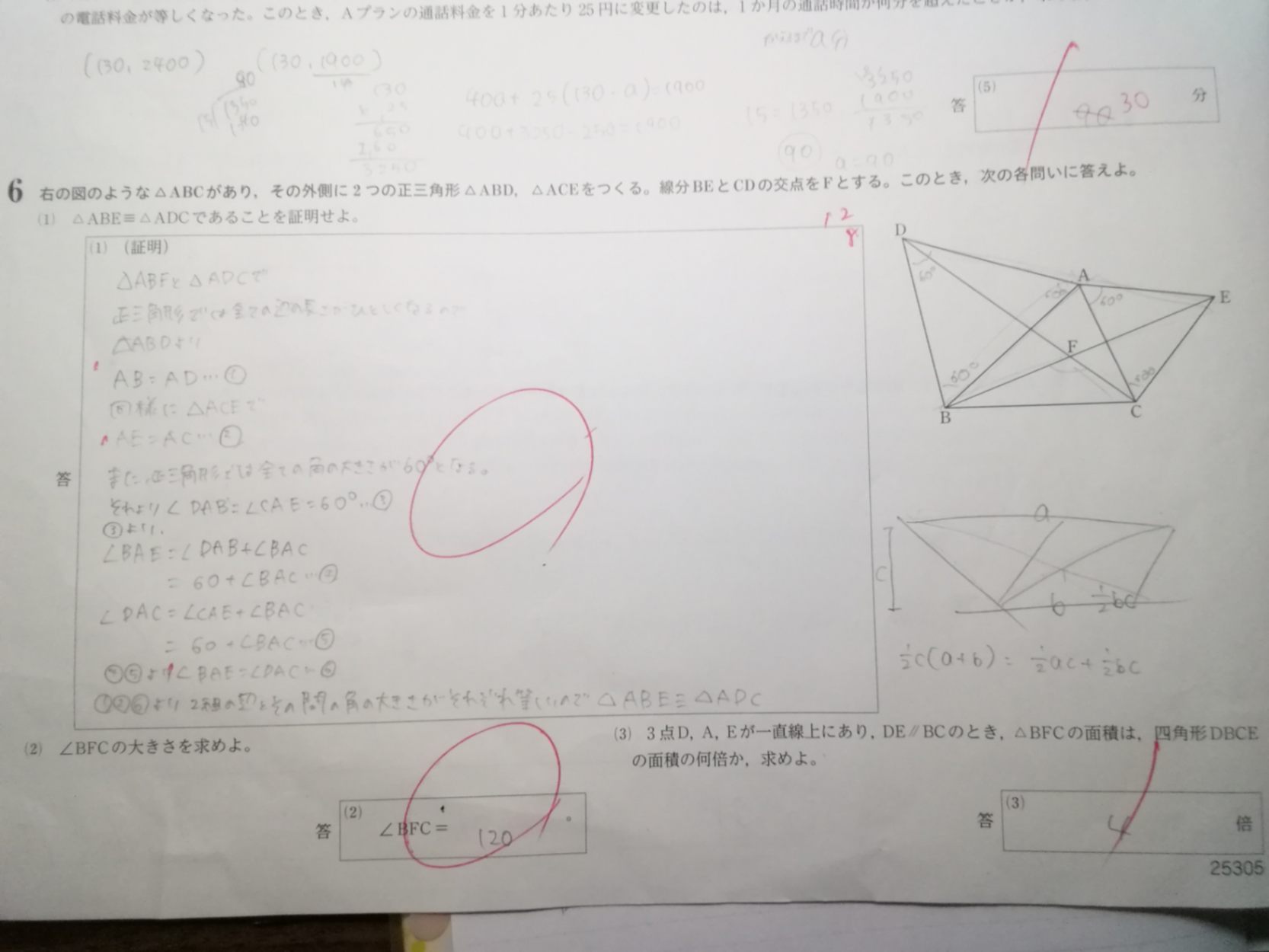
回答
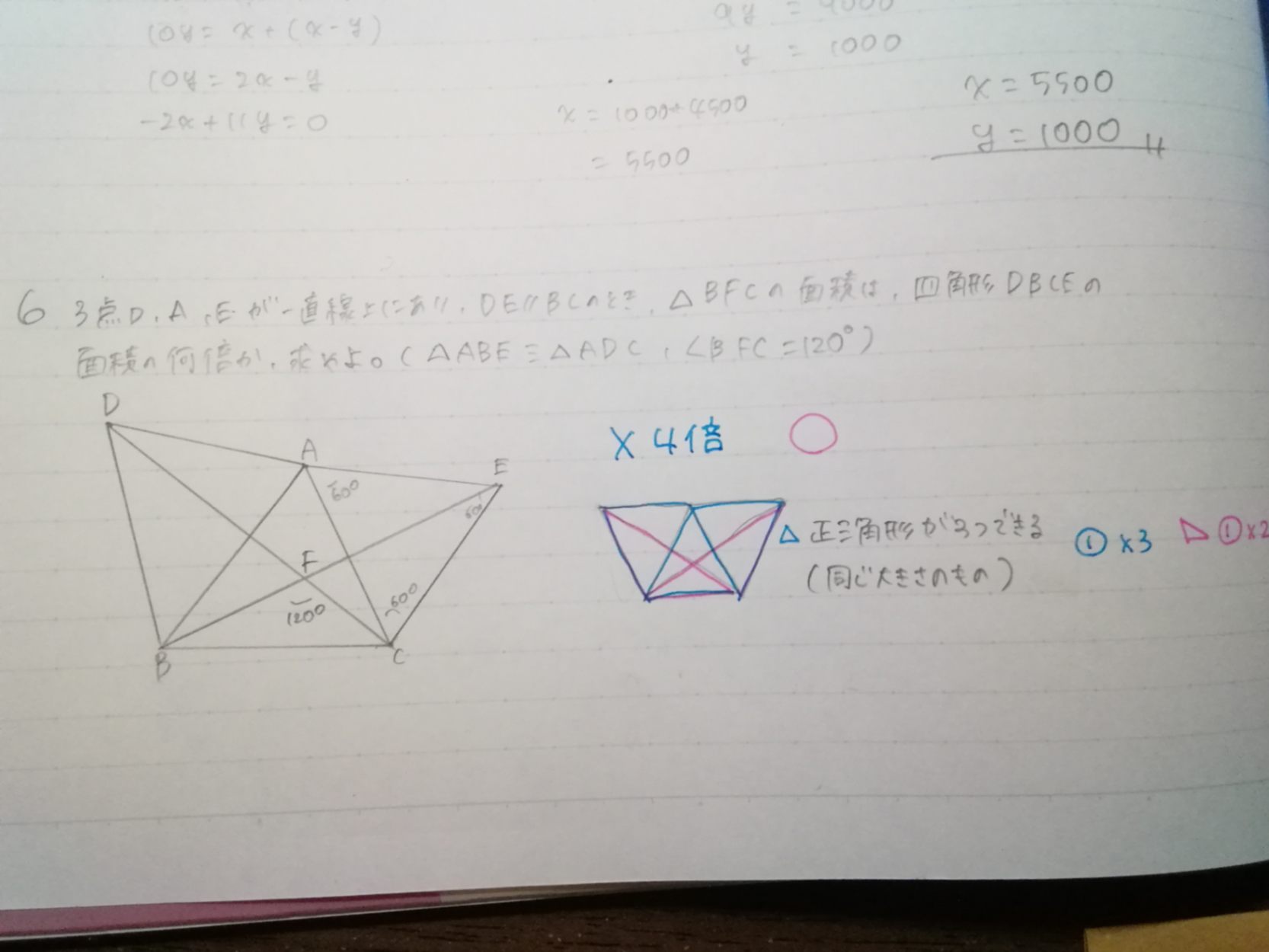
重心、…わかりません。笑 4倍はありえないですよね。時間が迫ってる中で解いたので多分頭がおかしくなったのかと… おまけは先生が証明に絶対ついてくるからとつけた名前です笑
上の回答に追記しました。読んでください。
まだ中点連結定理というものも習ってないんです😭 でもなんとなくわかりました!ありがとうございます! たぶん先生も解説してくれると思います…笑
そうか、中点連結定理も相似もこれから習うのかな? はて、その状態でどうやって説明できるのかなぁ? 先生の解説をしっかり聞いてください。 できればそのあと、コメント欄で先生のやり方を教えてくれませんか?
△DFEと△BFCを比べて2:1だからAF:JF=2:1とでもやるのかも。 相似は習ったのかな?
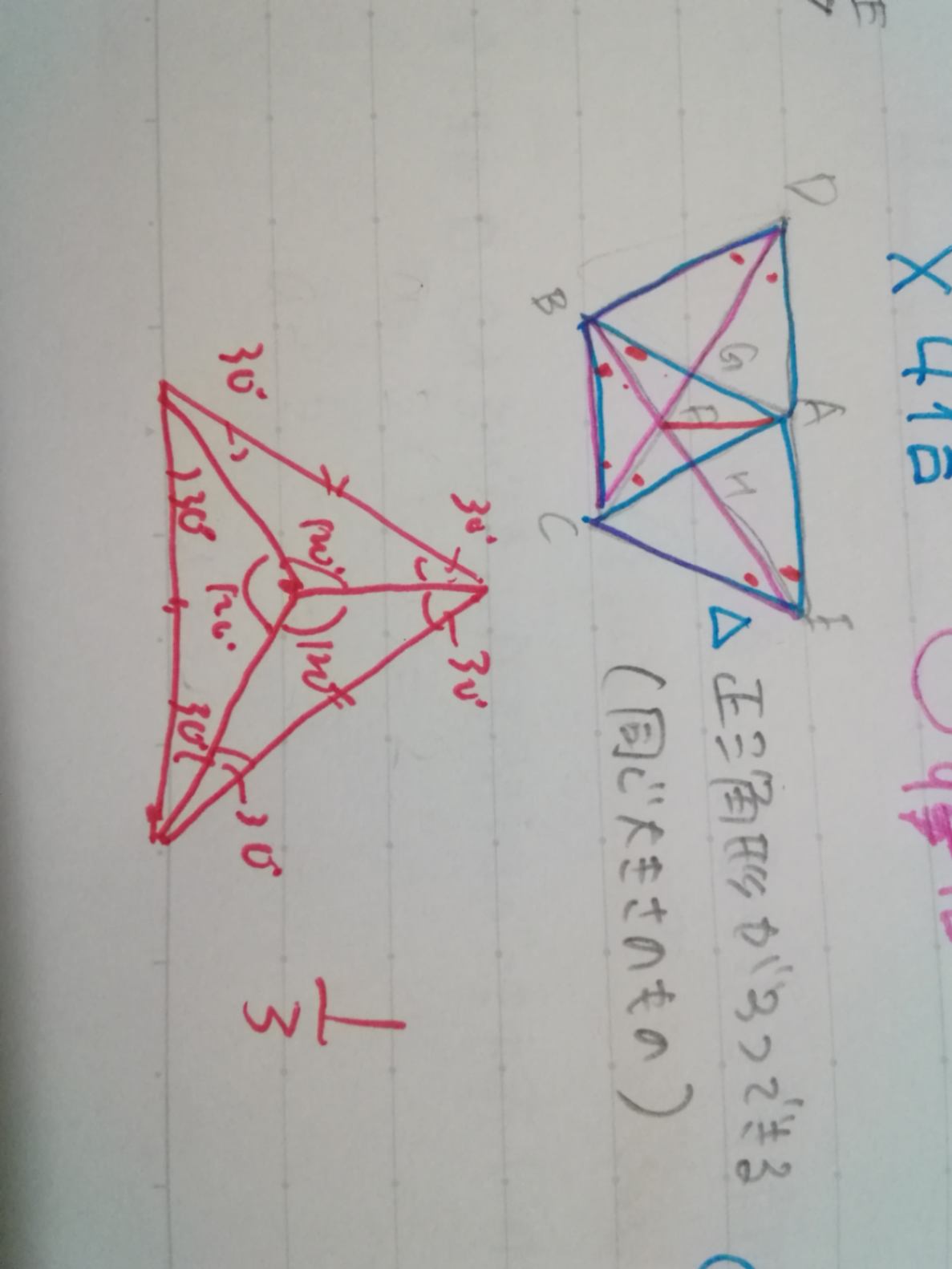
相似もまだなんです、笑 先生に聞いてみたら写真のようになると教えてくれました。ひし形ABCEの対角線がEBなので△BCEは二等辺三角形になります。反対側のひし形ACBDでも同様に△BCDが二等辺三角形になるので写真のように∠EBC=∠DCBとなります。このとき正三角形なので二等辺三角形の底角は30°になります。 正三角形のなかに底角30°の二等辺三角形は写真のように3つできるので面積は3分の1になるとのことです。 文字見にくいかもです。。
なるほど!そういうことか!難しく考えすぎでした。ありがとうございました。
あれ?赤い正三角形の一番上の30°30°、あるいは中心の120°120°はどうやって分かったのかなぁ?
あ、△ABF≡△ACFから分かりますね。上のコメントは無視してください(恥)。
笑 先生でも初めどう解くかわからないって言っていました笑
笑!