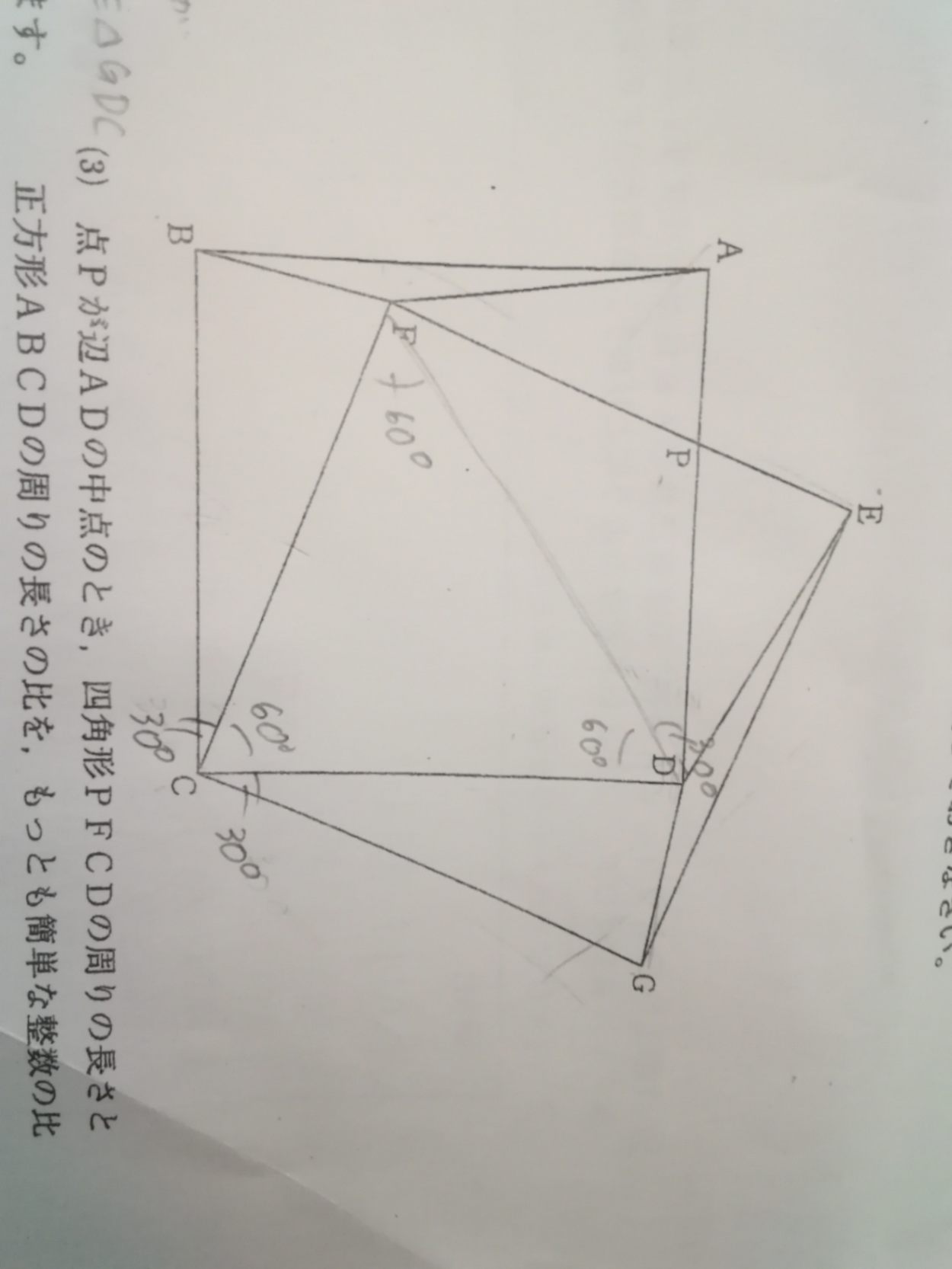
証明　面積

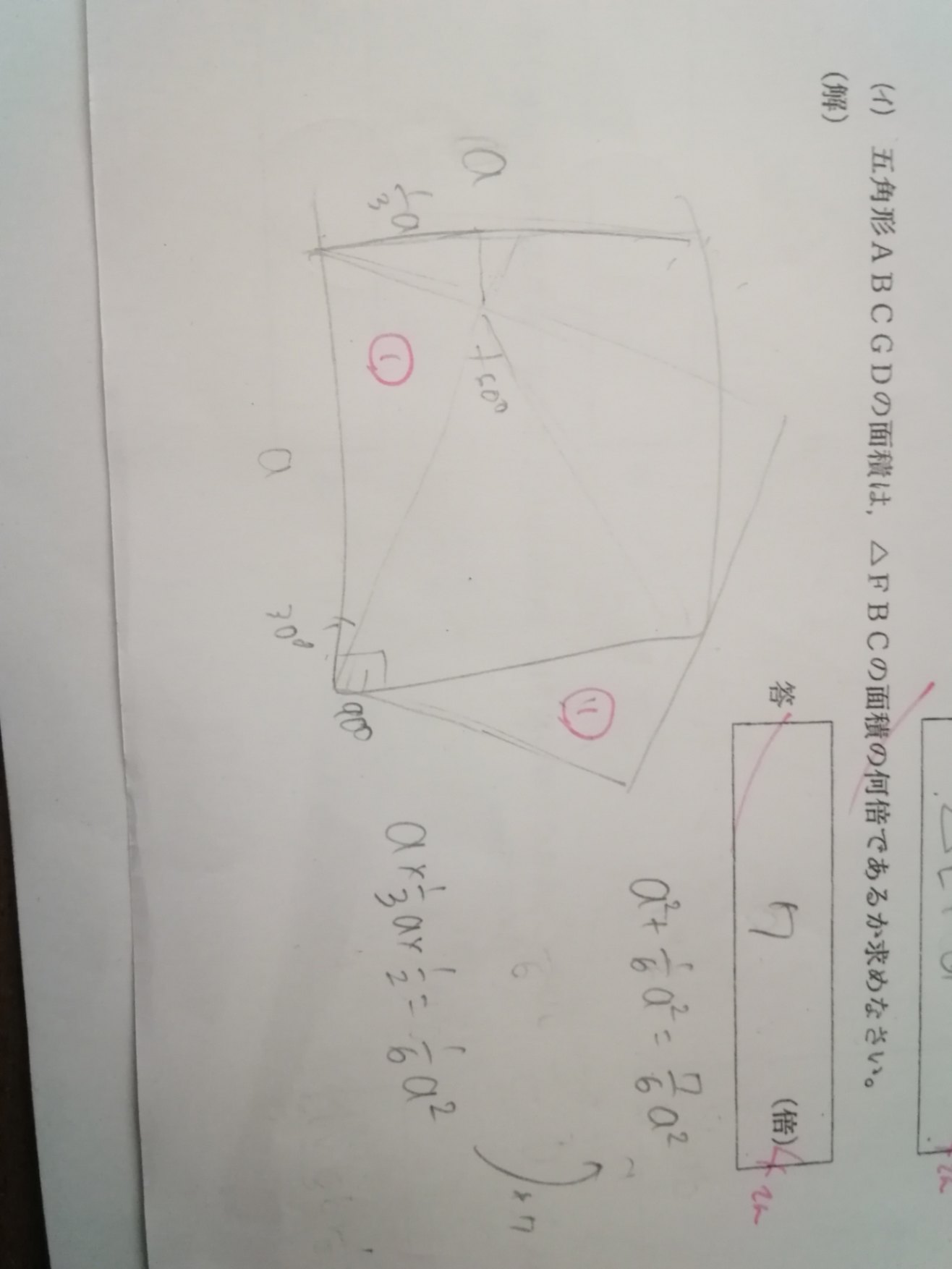
証明についてくる面積の求め方についての質問です。 いつも私は文字に置いて考えてるんですけどこれでは答えが間違ってしまって、 1/3aは∠BCDが90°だから30°はその3分の1になるだから高さも3分の1になるのかなっと想って解きました。 答えは5倍でした。解説よろしくお願いします。

かえでさん、こんにちは。 角度の大きさと長さは比例しません。そこは気を付けた方がいいです！ 正方形の1辺の長さをｔとしておきます（aにしたいのですが、あなたがaはもう使っているので笑）。 △DCGについて調べますよ。 底辺をDCと考えます。長さはｔです。あとは高さが知りたいです。 で、Gから底辺DCに垂線を引きますよ。GHとします。 ここで、△GHCは∠H＝９０°で、残りが３０°６０°の直角三角形になります。 このときGH＝$\dfrac{1}{2}GC$ であることは知っていますか？ （その図ではそうは見えないけれど、図の３０°が実際より小さく書いてあるんだね） 相似の最初の方でやるかなぁ。でも相似はまだやってないんだっけ？ 説明を書きます。別の三角形です。 正三角形XYZがあります。XからYZに垂線XWを引きます。するとその垂線XWは元の正三角形を真っ二つ２切りますね。 つまりWはYZの中点です。よってYW=$\dfrac{1}{2}YZ$ なんです！ △XYWは３０°６０°の直角三角形ですよ。 もとにもどります。 よって△GDC=$\dfrac{1}{2}DC\cdot GH=\dfrac{1}{2}\cdot t\cdot \dfrac{1}{2}t=\dfrac{1}{4}t^2$ 正方形の面積はt²だし、これで5倍になるのはわかりましたか？ コメント欄になにか返事を書いてください。よろしく。 あ、別な考え方！△FCDは正三角形ですね。Fを通ってBCに平行な直線を引けばDCの中点を通りますね。すると△FBCの高さはCからその中点までの距離ですから、1辺の半分です。これで△FBCの面積が正方形の1/4だと求められます。△DCGは△FBCとおなじです。