このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
三角関数
お久しぶりです🙇♀️
(3)までは解けたのですが、(4)がわからないです。
よろしくお願いします🙇♀️

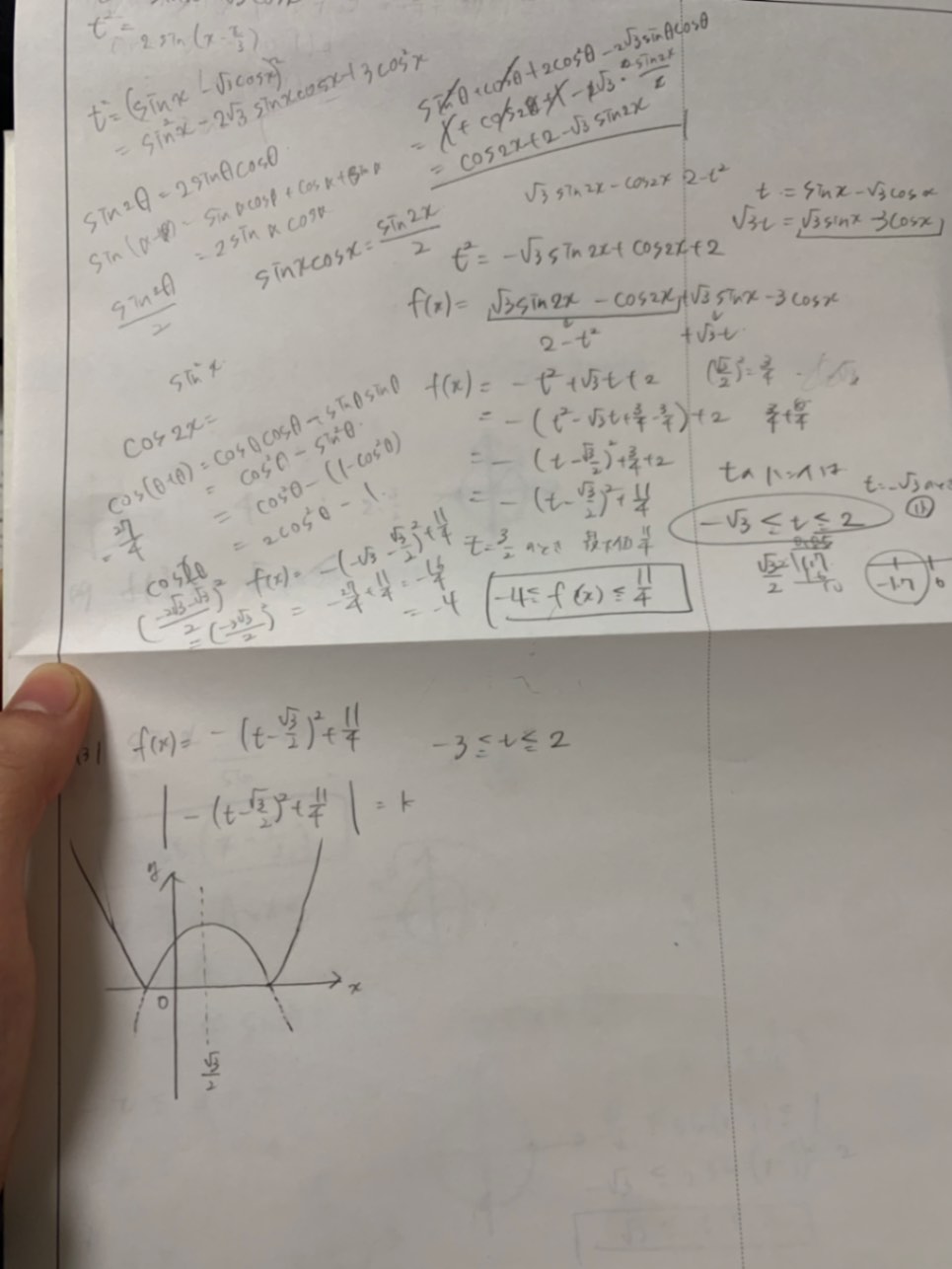
回答
百花さん、こんばんは。お久しぶりです!お元気出したか?
(4)???
ひょっとして(3)かな?
まず、あなたのグラフですが、範囲は $-\sqrt{3}\leqq t \leqq 2$ の範囲だけしか存在しません。
それから、端点は $t=-\sqrt{3}$ のとき $y=4$、$t=2$のときy=$2\sqrt{3}-2$ ですね。
またt軸との交点は $t=\dfrac{\sqrt{3}\pm \sqrt{11}}{2}\fallingdotseq 2.5,-0.8$ なので、
$-2<-\sqrt{3}<\dfrac{\sqrt{3}-\sqrt{11}}{2}<0<\dfrac{\sqrt{3}}{2}<2<\dfrac{\sqrt{3}+\sqrt{11}}{2}$
であることを押さえておいて、グラフの略図を書きましょう。
あとは、このグラフとy=kという水平な直線との交点のt座標が、tに関する方程式の解となります。
ところで$t=2\sin\left(x-\dfrac{\pi}{6}\right)$ ですから、tの値1つに対して$x-\dfrac{\pi}{6}$ は2つ決まってきます。
唯一の例外がt=±2となるときで、この時はサインの値が±1なのでxは1つしか出てきません。
この辺りを考慮すると、水平な直線が頂点のちょっと下を通るときはtの解は3つで、それらは2ではないので、xの解は6個でてきます。
水平な直線がグラフの右端を通るときは、1つの解が2となるので、xの解は5個になってしまいます。よってグラフの右端のちょっと上を通るところまでがxの解が6個ある範囲です。
よって $\dfrac{11}{4}<k<2\sqrt{3}-2$
と、解いたのですが、計算間違いがあったらお許しを。訂正してください。
これで大丈夫ですか?コメントよろしく。
出典はなんですか?どこかの模試?
(追記: 2025年10月30日17:20)
すみません、訂正します。
$-\dfrac{\pi}{6}\leqq x-\dfrac{\pi}{6}\leqq \dfrac{8}{6}\pi$ なので、
$\sin\left(x-\dfrac{\pi}{6}\right) <-\dfrac{1}{2}$ のとき、すなわち $t\leqq -1$ である解からは、xは一つしか決まらないようなので、直線y=kとも交点のうち一番左の解tからはxは1つしか求まりません。
よって答は「xの解の個数の最大値は5個。その時のkの範囲は $2\sqrt{3}-2<k<\dfrac{11}{4}$ 」…かな?
模試の解答が配られるのを待ちましょう(汗)
ありがとうございます! ここって左右反対ではないでしょうか?(下から五行目) 間違っていたらすみません 出典は模試です!
あ、反対です!ゴメン。 で、解法はわかりましたか?
kの範囲を求めるところまでしかわかりませんでした💦 実数解の個数の最大値という問題文の意味がいまいちわからないです
すみません。追記で訂正しました。