このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
青チャート 積分🙇
この問題が解答を見ても全然わかりません。立体をイメージできないから断面で考えるというのはわかりましたがなぜ画面に垂直な方向で積分するのですか？また、基準軸を決めた後も何をしているのかわかりません！
回答
ｈｋさん、こんにちは。
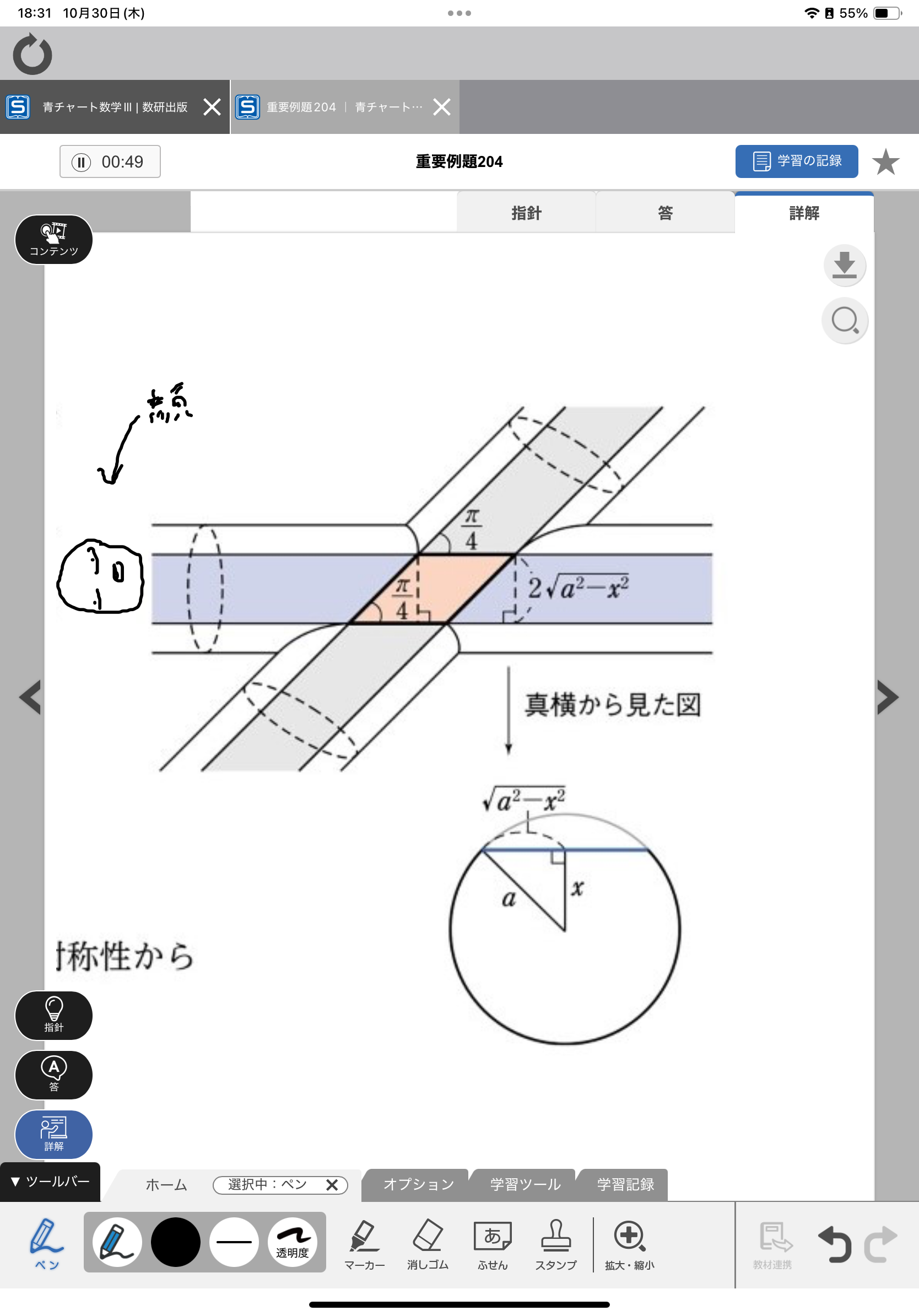
「なぜ画面に垂直な方向で積分するのですか？」…中心線の交点から中心線が作る平面に垂直な方向の直線が、交差した2本の円柱の対称軸、ひいては共通部分の対称軸になっているからです。この方向に積分するのが計算が楽なのです。
ほかの方向、たとえば2本の中心線が作る角の2等分線に沿って積分するというアイデアもあるかもしれませんが、その線に垂直に切ったときの断面（積分すべき面積）の形がとても分かりにくいですね。そこを解決できれば、その方向に積分するという解法もあるのでしょう。しかし、やはり解答の方向に積分するときが、断面積がひし形という単純なものになるので、計算はぜんぜん楽です。
「なぜ」という質問に対しては「その方向が計算が楽だから」としか答えられません。その方向でなければ絶対できないということないと思います。
要は、簡単に断面積が求まるのはどの方向に切ったときかを見極めることですね。
一番下の図のように、中心線からｘだけ離れた平面で円柱を切ったときの断面はその方向からは青い線として得られ、円柱全体を見れば長方形になるのはわかりますか？その上の図の青い長方形（無限に長いですが）です。もう一本の円柱を同じ平面で切ったらおなじく長方形が切り口で、灰色に塗った長方形になっています。りったいの共有部分は、部分的に見ればその2つの長方形の共有部分になりますので、それはひし形になります。切り取る位置（高さつまりｘの値）によって大きさは変化しますが、ひし形であることは変わりありません。
ひし形の面積はｘの関数になるのでｘで積分すれば体積になりますね。
これで大丈夫ですか？コメント欄になにか返事を書いてください。よろしく。
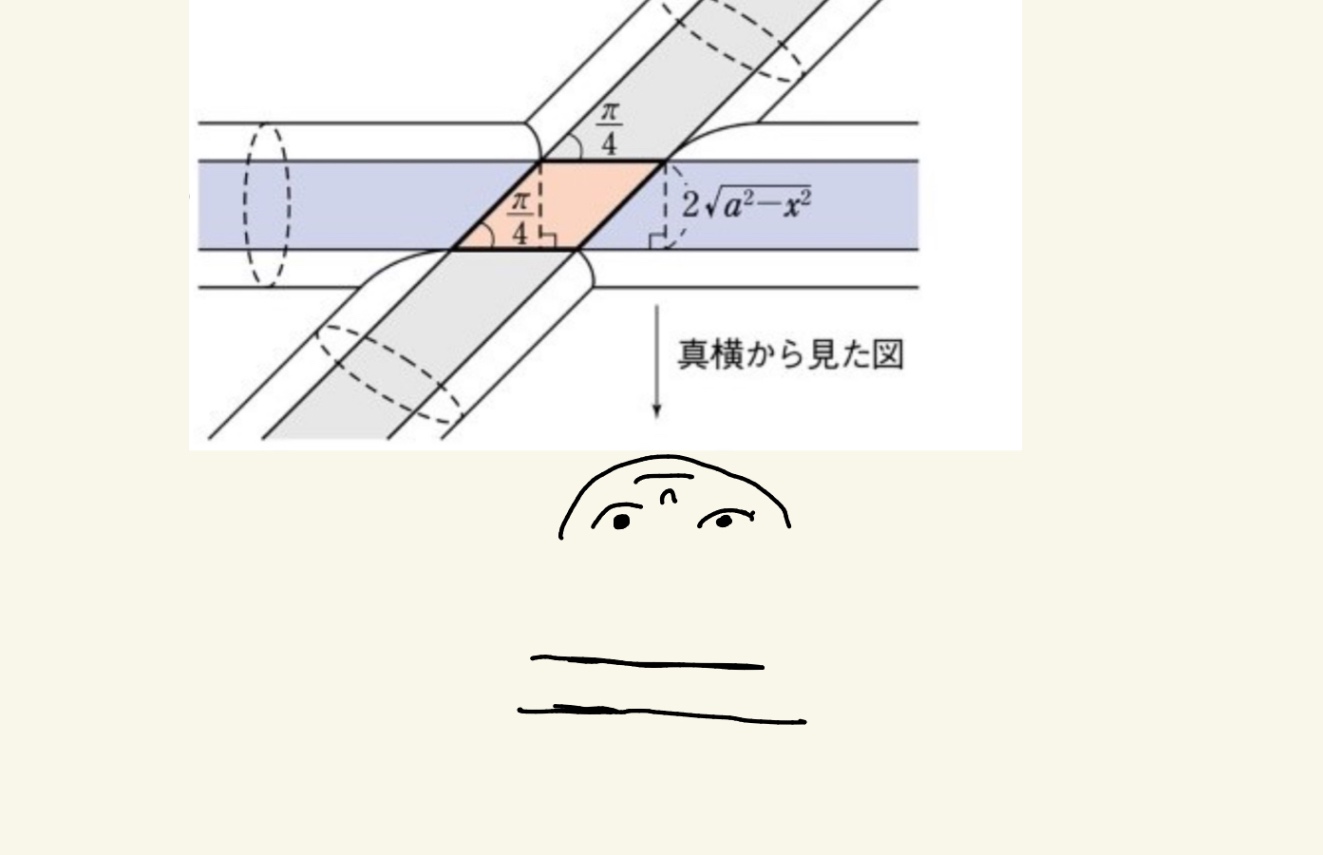
真横からというのはこういう見方ですよね？ 図の赤部分を取った感じですか？
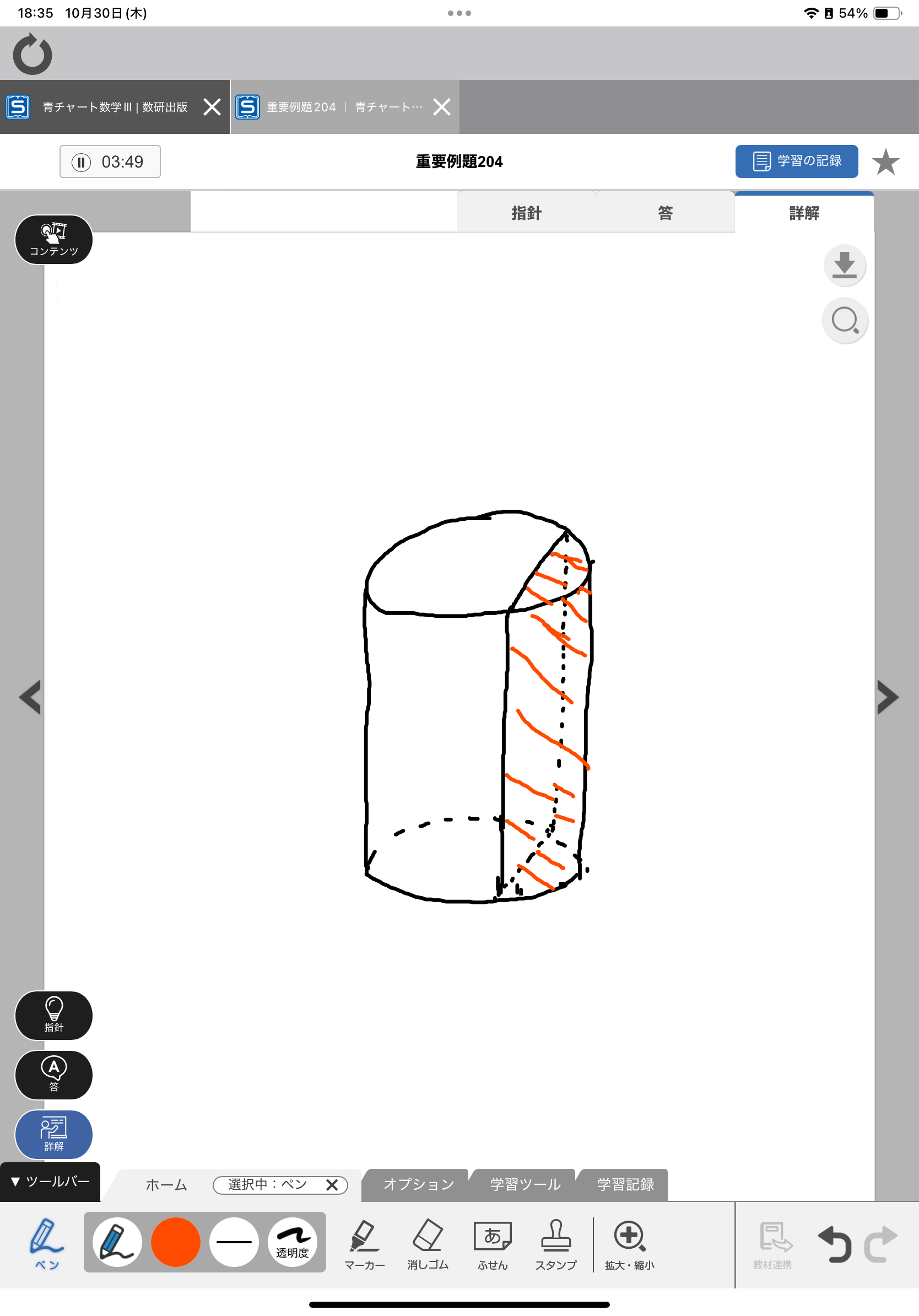
２枚目の写真にある「真横」というのはそうではないです。 水平な机に（寝かして）置かれた長～い円柱を途中で切ったその切り口ということです。 真横というのは円柱の中心線の伸びる方向から、という意味です。 赤部分を切り取るとかではなく、あなたの図の切断面が問題になっています。ほんの図では円柱は横倒しになっていて、水平に切ったときの切断面が青や灰色の（無限に続く）長方形ですよ。その赤い部分を切り取ったら２枚目の写真の図の交差する長方形が見えることは確かですが。
私へのコメントはここではなく、私の回答の下のコメント欄でお願いしますね。