このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
等差 等比数列
どのように解くかの方針すら立たないです。
現在高校2年 数列、漸化式学習済み
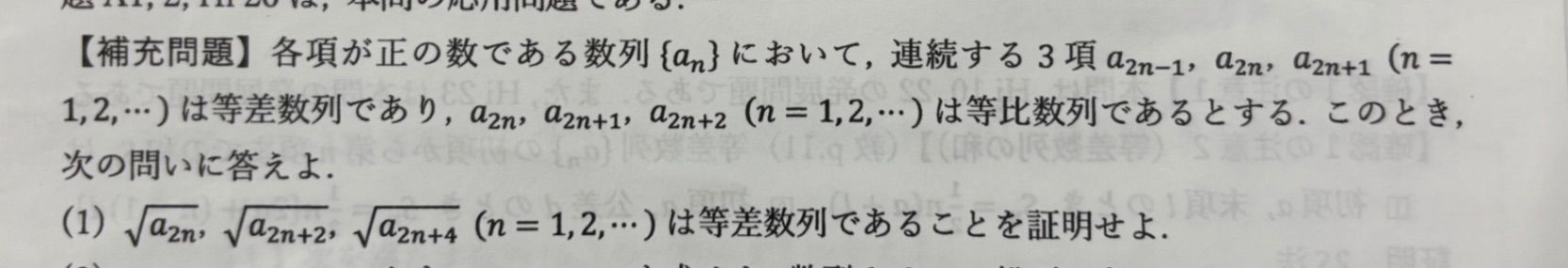
回答
問題の条件を整理してみました。
a[2n+1]=k1 + a[2n] = r1 * a[2n]...(a)
a[2n+2]=k2 + a[2n+1] = r1 * a[2n+1]...(b)
a[2n+3]=k2 + a[2n+2] = r2 * a[2n+2]...(c)
a[2n+4]=k3 + a[2n+3] = r2 * a[2n+3]...(d)
k1 -> r1 -> k2 -> r2 -> k3 -> ...という順番で繋がっているので、r1をk1で、k2をr1でというように左から順番に式にしていくことを考えます。
(a)よりr1 = (k1 + a[2n])/a[2n]
(b)よりk2=(r1-1)a[2n+1]=r1(r1-1)a[2n]
(c)よりr2 = (k2 + a[2n+2])/a[2n+2]={r1(r1 - 1)a[2n}+a[2n+2]}/a[2n+2]
a[2n+2]=r1^2 * a[2n]より、r2=r1(2 * r1 - 1)/r1^2
ここでa[2n+2]やa[2n+4]の表し方は複数ありますが、a[2n+2]=r1^2 * a[2n]、a[2n+4]=r2^2 * a[2n+2]の形のほうがルートをとったときに綺麗になりそうので、こっちで考えると
√(a[2n+2])=r1√(a[2n]) = √(a[2n]) + (r1 - 1)√(a[2n]) ... {無理やり等差数列の形に持っていく}
√(a[2n+4])=r2√(a[2n+2]) = √(a[2n+2]) + (r2 - 1)√(a[2n+2]) = √(a[2n+2]) + {(r1^2 - r1) / r1^2} * r1√(a[2n]) = √(a[2n+2]) + (r1 - 1)√(a[2n])
となって等差数列の形が出てきました。
書いてから気づきましたが『(a)よりr1 = (k1 + a[2n])/a[2n]』の部分は全く使っていませんでした……
着想としては
a[2n+2]=r1^2 * a[2n]、a[2n+4]=r2^2 * a[2n+2]がルートの計算に都合が良いと気付き、r2をr1で表すことを目標に進めるのが自然だと思われます。
個人的にはパズルのようで続きが気になる面白い問題でした!